PRIO, the Peace Research Institute of Oslo, jointly with the University of Oslo, organises a series of Oslo Lectures on Peace and Conflict, and their invited speaker in January 2018 was Aaron Clauset (University of Boulder, Colorado). In the ensuing panel discussion, where I took part, along with war-and-conflict researchers Håvard Hegre and Siri Aas Rustad, proper attention was paid to the partly controversial question mark in his talk title, Towards a More Peaceful World?. It is controversial, since we would prefer it to be a !! instead, and since there is extensive work, in vivid prose and with dry facts and neutral analyses, indicating that The Better Angels of Our Nature are slowly winning.

Clauset rather argues that the war world history is still essentially stationary, to an almost amazing degree, and that we can't yet assert that the violence is in decline. In statistical parlance, he's not yet rejecting the big null hypothesis $H_0$ that the violence degree for interstate wars has been essentially unchanged, over the past two hundred years – he explains, rather, that it might take him another hundred years to agree with the Pinker view of the world. This blog post addresses some of these statistical concerns (using the same dataset, on the number of battle deaths for wars), and reaches partly different conclusions.
Correlates of War (and Statistics): Battle Death Numbers for 200 Years of Wars
High-quality data on wars through history are being collected by several parties, including PRIO and ViEWS (a political Violence Early-Warning System at Uppsala). The Correlates of War project seeks quite generally and ambitiously to facilitate the collection, dissemination, and use of accurate and reliable quantitative data in international relations. The particular dataset worked with in Clauset's papers, and which I will discuss here, can be suitably squeezed out from one of the CoW boxes of data, and consists of
\((x_i,z_i)=(\hbox{time of onset, number of battle deaths}) \)
for $i=1,\ldots,n$, with $n=95$ severe wars, being fought from 1823 to 2003; the lower threshold at use here is 1000 dead, so each $z_i\ge1000$.
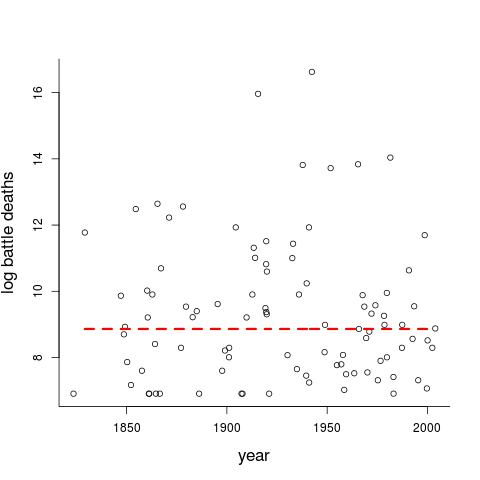
Clauset's basic story telling ingredients relate to these particular data, and hence to this particular figure, which features the war onset times (from 1823.27 to 2003.22, as we operate with dates, not merely years) and log-counts $y_i=\log z_i$ (ranging from $6.908=\log 1000$ to the horribly high numbers 15.695 and 16.627, for World Wars I and II; you may exp them to get back to the original bloodier scale).
I will comment on the red threshold line indicated in the figure in about two minutes, but first briefly address a few basic issues which belong to these types of discussions. There are certain general questions relating to how one interprets the data, and the extent to which one might be willing to build and fit statistical models, for analysis and prediction purposes.
- One view voiced here is that the statistical data points above represent unique and dramatic stories, with their own mechanisms and weapons and historical components, and with tentative definitions and labelling changing under our feet. So, the argument goes, since a war is not a war is not a war (this is where one may be allowed to say "and what about terrorism?" or "an atom bomb [God forbid] will change all equations"), and with measures of democracy and institutional impact and demography and public health etc. also having changed dramatically, we should turn to concepts and tools of history and political science and sociology to catalogue and understand each war, but not look too hard for statistical patterns, common types of behaviour, testing number-driven hypotheses, forming predictions, etc.
- Another view is the more statistical one, to admit that we do not pretend to understand each data point fully or particularly well, but data are data, information is information, well-fitting statistical models can be built (and statistically verified), and used (a) to identify patterns and significant mechanisms; (b) to help interpret the past; and (c) to make intelligent data-driven predictions for the future.
While I do have sympathy for many of the arguments used by Camp One here, see e.g. Østerud (2008), I belong (not surprisingly) to Camp Two, willing to and able to fit well-working statistical models, to help seek out potentially interesting patterns and mechanisms appearing to be at work for our complex world, and to form intelligent predictions for the future, say for the coming 50 or 100 years. As Pinker notes (Better Angels, Ch 5), discussing matters which match my Camp One vs. Camp Two here, "More than half a century later, we know that the eminent historian was wrong and the obscure physicist was right". I dare to say that Pinker oversells the latter point a bit here, though, to make his (valid) point more forcefully than strictly necessary – Lewis Fry Richardson (1881-1953) was not at all "obscure", but an eminent polymath (mathematician, meteorologist, physicist, chaos theorist, pre-Mandelbrotian fractalist, FRS, and, indeed, first rate statistician). His data, models, and predictions have been instrumental for pushing war-and-conflict analyses to the research front, and his conclusions and insights regarding wars and conflicts have indeed proved themselves to fare much better than those of Arnold J. Toynbee (1889-1975).
Now back to the $(x_i,z_i)$ figure above, which I proclaim being willing (and able) to examine from a statistical modelling and interpretation perspective – as is Clauset. Also important for the statistical story telling and drama interpretation is the red threshold indicated in the figure, namely $y_0=8.862=\log 7061$. The interpretation is that the number of fatalities $z$ follows a statistical power-law distribution, of the type $f(z)$ proportional to $1/z^\alpha$, for all wars with $z$ above a threshold $z_0$. The $\alpha$ tail index parameter is of primary importance, as it purports to accurately describing the behaviour over time of all really bloody wars ... also in the future, if the world continues to behave approximately as in the past. So, via a certain estimation algorithm (one out of several possible methods, actually), Clauset has found $z_0=7061$, with 51 sufficiently extreme wars above this threshold (and 44 wars hence falling below).
The Stationary View
A simple (but rather robust) statistical view of the data above is that the world is (fully or nearly) stationary:
- the inter-war times $d_i=x_i-x_{i-1}$ are i.i.d. (independent and identically distributed);
- the sizes $y_i=\log z_i$ are also i.i.d., and independent of the inter-war times.
There are certain common and more specific versions of these two statements, related to concepts of `full but stationary randomness over time', as for Poisson processes (and marked Poisson processes) with constant rates. So a schoolbook model (well, university stat course #3, perhaps) says (i) that the inter-war times $d_i$ are ${\rm Expo}(\lambda)$, i.e. exponentially distributed with some parameter $\lambda$, with density function $\lambda\,\exp(-\lambda d)$, and (ii) that the $y_i$ come from a common density, say $f(y,\theta)$. Clauset does not go into the full modelling of $y_i$ (in that case, via his $z_i$ to my $y_i=\log z_i$), and is content to care for the upper tail, via the $\alpha$ parameter and the proportional to $1/z^\alpha$ power law. An easy technical argument shows that this is equivalent to saying that the $y_i$ above a certain threshold $y_0$ follows the exponential density
\(g(y)=\theta\exp\{-\theta(y-y_0)\} \quad \hbox{for}\ y\ge y_0,\)
where $\theta=\alpha-1$. So, Clauset's model is stationary, rather simple (it can be taught and worked with in a bachelor level course), and has three basic parameters: the between wars intensity $\lambda$, the threshold $y_0$ (or $z_0=\exp(y_0)$, in his $z$ story telling modus), and the tail index $\alpha$.
Let me briefly comment on two statistical details, inside this statistical `the world hasn't changed' view of stationarity, pertaining to aspects (i) and (ii) above, before I look for signs of optimistic departures from that description. Panel (i) below displays a quantile-quantile plot for the inter-war differences $d_i$, where the ordered data ought to follow the dotted straight line under the ${\rm Expo}(\lambda)$ assumption. The plot indicates that the model is quite good, but not perfect. A somewhat better fit is provided by the mixed-up exponential view that the $d_i$ rather follow a density like
\(h(d)=\int\lambda\exp(-\lambda d)\pi(\lambda)\,{\rm d}\lambda\)
for a suitable mixing density $\pi(\lambda)$. Specifically, the spacings data $d_i$ are well described via an exponential with fixed parameter $\widehat\lambda=0.522$, but a bit better described via a $\lambda$ that varies over time, according to a gamma density with mean 0.607 and standard deviation 0.223. Panel (ii) relates to the statistical problem of not merely estimating the $\alpha$ tail index parameter, the one governing the extreme wars, but also quantifying its uncertainty. As such the confidence curve ${\rm cc}(\alpha)$ given there, constructed via methods developed in the Schweder and Hjort (2016) book, gives confidence intervals at all levels. This is more accurate than quoting the usual format of point estimate with a 95% interval, which here is $1.525\pm0.073$ (which is what Clauset finds), also because the confidence curve is not entirely symmetric.

One more point of statistical delicacy is that of describing the tail of the $z_i$ distribution (or, equivalently, the $y_i$ distribution). The theory of extreme value statistics might be used to argue that the $v_i=y_i-y_0$, for those above the threshold $y_0$, could follow the statistical distribution with cumulative distribution function
\(G(v) = 1 - (1-a\theta v)^{1/a}\)
which is a delicate two-parameter extension of the simpler \(G_0(v)=1-\exp(-\theta v)\), the limiting case $a\rightarrow0$, and which corresponds to exponential tails (used above). This two-parameter distribution accurately describes the world's best 100 m races over many years, for instance, which I've analysed to ascertain just how surprised we ought to have been when Bolt set his world records. For the battle deaths data I've fitted this two-parameter distribution and found a rather small $\widehat a=0.072$, which turns out not to be significantly different from zero. In yet other words, the simpler power-law description for extreme wars is adequate.
Statistical Sightings of Better Angels
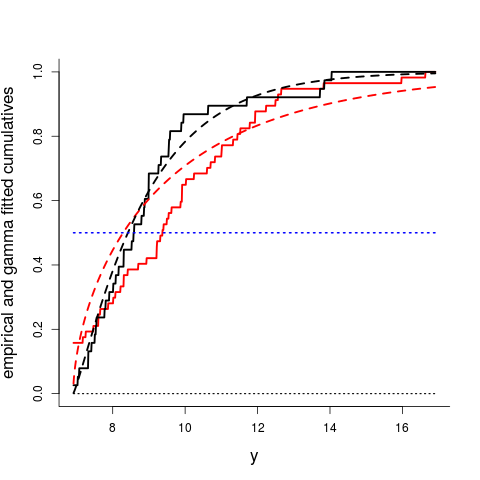
In the Clauset type analyses, attention is focused on the extreme part of the battle deaths distribution, those above the threshold for power-law behaviour. The full drastic list of 95 wars deserve to be modelled, however, not merely the 51 most extreme ones (for which $z_i\ge7061$, the power-law threshold). A somewhat simple and not fine-tuned choice is to take the $y_i=\log z_i$ as stemming from a Gamma distribution, dictated by its two parameters $(a,b)$. I can then fit the Gamma to all of the data, as well as to parts of the war list. The figure below displays the real cumulative distributions (qua non-smooth empirical cumulatives) and the Gamma fitted distributions (smooth curves), for all wars having started before 1945 (in red) and similarly for all wars started after that year (in black).
The difference between the two distributions is noticeable, though admittedly not on the drastically significant side. You would probably prefer to live after 1945, if given the choice, since the pre-ww2 red curves fall to the right of the post-ww2 black curves. The medians for the pre-ww2 and post-ww2 wars, where the curves cross 0.50, are 9.377 and 8.581, on the $y=\log z$ scale, which when exp'd corresponds to 11808 killed and 5330 killed, respectively, hence indicating a drastic difference. A model selection analysis, using e.g. the Akaike Information Criterion AIC, shows clearly that Gamma modelling with two + two parameters (pre and post 1945) gives a better statistical description than with two parameters (treating all 95 wars as being stationary in size). More delicate model building and model selection issues can be worked with via the Focused Information Criterion FIC, via the methods developed in Julllum and Hjort (2017).
Changepoint Detector Detects the Vietnam War
Since analyses of the above type indicate that the World of Wars might not have been entirely stationary after all, potentially with some Better Angels at work, we might search for a breakpoint in the distribution of battle deaths over time. Such searches for change-points and regime-shifts can be arranged in several ways, depending upon the models used and on the (many) ways in which a statistician can spot a difference between two distributions. Here I employ confidence curve methods developed for such purposes by Cunen, Hermansen, Hjort (2017), set to work on the $y_i$ above threshold $y_0=\log 7061$, where these have an exponential distribution. Subtracting the threshold leads to a case where observations $y_1,\ldots,y_{51}$ are seen to be from ${\rm Expo}(\theta_L)$ to the left and from ${\rm Expo}(\theta_R)$ to the right of a potential change-point $x_0$ in time. Our methods then yield not merely a sensible point estimate, but also a full confidence curve ${\rm cc}(x_0)$ for the potential change-point. Carrying out this led to the following plot in my PRIO presentation:
The plot yields a clear identification, not to the half expected 1945 (indicated with a vertical line there), but to ... 7 February 1965. This is the Vietnam War, or more precisely what in the CoW system is coded as the start of its Phase Two, with the attack on Camp Holloway. This is the point in time where the statistical difference between before and after is at its clearest. The confidence curve ${\rm cc}(x_0)$ says it's pretty sure that 1965 is a good candidate for a real change in sizes of wars, as measured through the lens of the tail index $\alpha$ for the extreme ones.
We may also investigate this separately, via the next plot, telling us about the 51 observed values of $v_i=y_i-y_0$, with 37 to the left and 14 to the right of Camp Holloway. The means for these two groups are 2.219 and 1.077, respectively (indicated with dashed lines). Yes, the ratio 2.059 is properly significant, with a p-value of 0.007, via the appropriate F distribution. In terms of the tail index parameter $\alpha$ of the proportional to $1/z^\alpha$ for extreme wars, these statements translate to the world view that $\widehat\alpha_L=1.451$ and $\widehat\alpha_R=1.927$, before and after the Vietnam War, give a better overall description than saying that the same $\widehat\alpha=1.525$ has been in force since 1823 to the present. So there's hope that we've changed, slowly, for the better, even when looking at the brutal raw counts of battle fatalities.
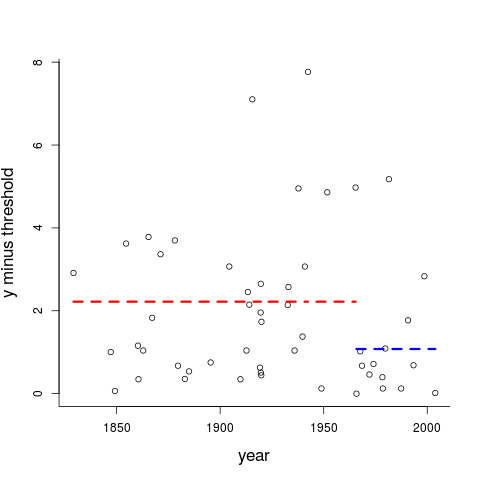
The above analysis should count as good statistical evidence that the distribution of battle deaths over threshold has not remained stationary, from 1823 to the present, with the p-value of 0.007 when comparing before and after the Vietnam War in the above model formulation as particularly convincing. We ought to be careful regarding such conclusions and interpretations, however; the change in tail index level can't be expected to have been quite as abrupt as the somewhat simple change-point envisages. The Vietnam War Plot also tells us that the statistical high-level confidence sets need to be very wide.
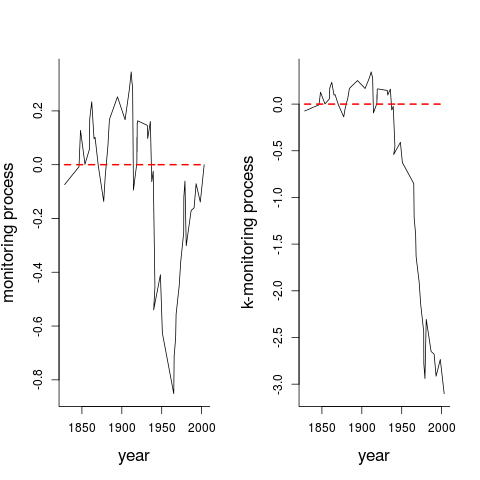
Even though I might risk overexplaining or even overanalysing some of these Vietnam War change-point story features, I choose to include one more pair of plots. These are monitoring process plots, applying methodology of Hjort and Koning (2002). Here they are shown at work for the particular exponential model situation of $v_i=y_i-y_0$ over threshold, but they are meant to be useful tools when searching for and establishing the presence of change-points also in more general setups than the present. In Panel (i) I display the monitoring process
\(M_n(t) = \widehat J^{-1/2}(1/\sqrt{n})\sum_{i\le [nt]} u(v_i,\widehat\theta) \quad\hbox{for}\ 0\le t\le 1, \)
but plotted for calendar time $x_i$ rather than $i/n$; here $u(v,\theta)$ is the score function of the model and $\widehat J$ the estimate of the Fisher information quantity $J(\theta)$. Under no-change conditions this Hjort-Koning monitoring process should vary smoothly around zero, across the time window considered, and its full process distribution is approximately that of a Brownian bridge. It also has the property that if there is a break-point, then it should have a "triangle with some noise" type shape around that break-point, and, lo & behold, this Hjort-Koning monitoring plot points precisely, again, to the Vietnam War. It then needs to be admitted that the size of the maximum absolute value of this plot is not impressive enough to warrant rejecting the $H_0$ hypothesis of no change, per se, partly because the $M_n$ plot is in overall checking modus, without any particular alternative to constancy in mind. In Panel (ii) a weighted version is displayed, of the type
\(M_n^*(t) = \widehat J^{-1/2}(1/\sqrt{n})\sum_{i\le [nt]} K_n(i/n)u(v_i,\widehat\theta) \quad\hbox{for}\ 0\le t\le 1, \)
for a weight function $K_n(\cdot)$ fine-tuned to pick up signs of such a change-point; see Hjort and Koning (2002) for details. The statistical persuasion point is that this second monitoring process $M_n^*$ displays behaviour outside the normal bounds under the no-change hypothesis (zooming in on the maximum absolute value, for example, yields a p-value of 0.06). Overall, these and the above analyses indicate that it is plausible that the world or wars have not been entirely stationary, and that Better Angels are at work, with a decline for the extreme wars taking place from the Vietnam War onwards.
Battle Deaths Per Capita
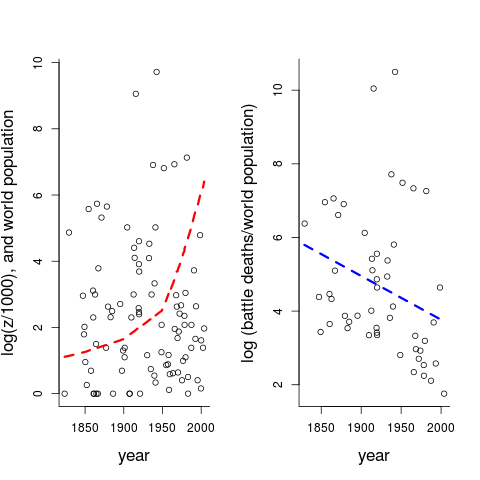
My analyses so far, like Clauset's, have been for the straight $(x_i,z_i)$ data, with battle deaths as the main quantity studied. However, losing 1 million [God forbid] for a world with 1 billion is worse than for a world with 10 billion, most of us would agree – if necessary by the probability calculus argument for the probability that you yourself, qua randomly sampled individual from this planet, will vanish in a war. It is hence natural to bring say $w_i$, the world population size in the year $x_i$ where the war was fought, to the table. It takes me about four minutes to find world population figures $0.978,1.262,1.650,2.518,4.068,6.070,6.909$ (in billions, i.e. $10^9$) for the years $1800,1850,1900,1950,1975,2000,2010$ – and then embarrassingly many minutes to R-code this into a piecewise linear approximation for the world population size, for all years from 1800 to 2010, and finally to match these properly with the war-onset-times $x_i$ (I'm sure there are better and more accurate ways in which to bring in the required $w_i$). Having achieved this, however, it is easy to construct the figure below.
Panel (i) shows the $\log(z_i/1000)$ numbers of log battle deaths, but now accompanied by the dashed read curve, which is the amazingly growing $w_i$ over time. Then going for the normalised $z_i/w_i$, essentially the per capita view of things, Panel (ii) displays the resulting $\log(z_i/w_i)$ points, along with the linearly decreasing blue trend line. This gives at least a more optimistic reading of the battle deaths data than for the non-normalised case. The decrease is statistically significant, and there are several ways in which to model this basic finding in somewhat more informative ways. I would pursue that theme too, if the aim is to construct clever predictions for the future, but I abstain from going there for this blog post; the present point is that the downward decrease of $z_i/w_i$ over time should count among the statistical sightings of the Better Angels.
Statisticians Against War
The FocuStat statisticians are no strangers to war (well, to a few statistical aspects of some wars, then). Céline Cunen's blog post on the Game of Thrones being compared to the Wars of the Roses (1455-1487) has been picked up by various media and has been discussed on the web in at least a dozen languages. Another FocuStat blog post, by Céline and myself, goes into a certain literary mystery concerning the World's First Ever Novel (written in Catalan, in the 1460ies), and the chief themes of that book are entirely war-like and war-related. Furthermore, Gudmund Hermansen (who is still with us for the part of his time, even after going from PostDoc to an associate professor position at BI Norwegian Business School) is working with Håvard Mokleiv Nygård at PRIO on a Research Council of Norway funded five-project to examine statistical aspects of conflict escalation. And one particular fruitful consequence of an official agreement between the University of Oslo and PRIO is that Håvard and I will jointly supervise Jens Kristoffer Haug, a properly Heidegger trained Master student, on another war-and-peace statistical study. Below, Jens and Håvard read Pinker (presumably The Long Chapter on The Long Peace) wheras as I felt a need to check up on Война и мир.

Photo: Bjarne Røsjø, from the Titan news article on the PRIO event, and where Håvard Nygård and I are being interviewed.
So what can we do, for modelling and understanding and contributing to war-and-peace statistics? The statistical challenges are in at least in some basic senses not too different from attempting to understand, model, assess, predict matters of climate change, or, for that matter, other Big Complex Things where it is not possible to understand all of what goes on, but where one nevertheless can carry out good, fruitful, statistical work. Two such cases of Big Complex Things that come to the FocuStat mind concern work some of us have been involved with, in respectively the Northeast Atlantic (examining the Hjort liver quality index of the Atlantic cod 1859-2013, along with influential factors) and the Antarctic (manoeuvring between whales and politics) – no, we can't fully understand all of the mechanisms at work, but yes, we can model and sort out and detect influential factors and predict.
It may be added here that the Statistical Toolboxes do not stop after having selected and fitted and tested and interpreted a model, but include methods of assessing uncertainty, finding out the degree of external variation, supplementing predictions with the proper bands of uncertainty, etc. Also, statistical modelling etc. become more fruitful (and more complex, and harder to carry out) when the war-and-peace datasets are considerably more complex than the somewhat simple $(x_i,z_i)$ set above. Successful statistical work involves fitting complex data (stemming from complex and partly not-yet-understood mechanisms) to models, and even when these are simpler than reality (no statistician would argue that two hundred years of interstate wars result from a four-parameter i.i.d. generator of onsets and body counts), they can still capture the essence (with the remaining variability also captured, in the implicit error terms of the models).
So, in view of the statistical modelling carried out here, with the tentative conclusions drawn – wouldn't it be nice if, as the B.B. so eloquently express it, indeed from precisely that point on our common species time axis, if the Vietnam War, identified in the Cunen-Hjort change-point plot above, quickly followed by the Flower Power of Sergeant Pepper and Woodstock, really turns out to be the Beneficial Breakpoint, the Charitable Change-point, the Generous Game-changer, the Radical Regime-shift, complete with a Before and an After attached to it, where the fundamentally cute but occasionally terrifying homo sapiens species has managed to become, well, significantly less warrying and violent and belligerent, than before?
Thanks
I've benefitted from ongoing discussions about these matters, models, and methods with fellow FocuStat-ers Céline Cunen, Gudmund Hermansen, and Emil Aas Stoltenberg, and look forward to more, also with Håvard Nygård and our student Jens Kristoffer Haug. Håvard helped me manouevre into the CoW datasets. I'm usually fully able to R myself through all necessary calculations and analyses and plots, if I have the required time on my hands – on this particular occasion, however, I was pressed for time, and Céline volunteered to implement and run the required Cunen-Hermansen-Hjort method for confidence curve change-point analysis for the exponential distribution (which was not on our earlier repertoire of models). The Vietnam War Plot pictured above is hence due to her last-hour-before-talk efforts. Finally I very much appreciated both reading through Aaron Clauset's stimulating papers and our ensuing discussions at PRIO (and at the dinner).
(Some) references
Boys, B. (1965). If, Wouldn't it Be Nice. CBS Columbia Square.
Claeskens, G. and Hjort, N.L. (2008). Model Selection and Model Averaging. Cambridge University Press.
Clauset, A. (2017a). The Enduring Threat of a Large Interstate War. OEF Research Report.
Clauset, A. (2017b). Trends and fluctuations in the severity of interstate wars. In press.
Cunen, C. (2015). Mortality and Nobility in the Wars of the Roses and the Game of Thrones. FocuStat blog post.
Cunen, C. and Hjort, N.L. (2016). Combining information across diverse sources: The II-CC-FF paradigm. Proceedings from the Joint Statistical Meeting 2016, the American Statistical Association, 138-153.
Cunen, C. and Hjort, N.L. (2017). New statistical methods shed light on medieval literary mystery. FocuStat blog post.
Cunen, C. and Hjort, N.L. (2018). Whales, Politics, and Statisticians. FocuStat blog post.
Cunen, C., Hermansen, G. and Hjort, N.L. (2017). Confidence distributions for change-points and regime-shifts. Journal of Statistical Planning and Inference.
Hegre, H. (2013). Peace on Earth? The future of internal armed conflict. Significance, 10, 4-8.
Hegre, H., Karlsen, J., Nygård, H.M., Strand, H., and Urdal, H. (2013). Predicting armed conflict, 2010-2050. International Studies Quarterly, 57, 250-270.
Hermansen, G., Hjort, N.L. and Kjesbu, O.S. (2016). Recent advances in statistical methodology applied to the Hjort liver index time series (1859-2012) and associated influential factors. Perspective Paper, Canadian Journal of Fisheries and Acquatic Sciences, 73, 279-295.
Hjort, N.L. (2015). On just how surprised we ought to have been when Bolt set his world records. Talk at the Norwegian Statistical Meeting, Solstrand.
Hjort, N.L. and Koning, A. (2002). Tests for constancy of model parameters over time. Journal of Nonparametric Statistics, 14, 113-132.
Hjort, N.L. and Schweder, T. (2017). Confidence distributions and related themes. Editorial overview, for a Special Issue of the Journal of Statistical Planning and Inference, with Hjort and Schweder as guest editors.
Jullum, M. and Hjort, N.L. (2017). Parametric or nonparametric: The FIC approach. Statistica Sinica, 27, 951-981.
Our Nature, Angels of (2011). The Better. Penguin Science.
Pinker, S. (2012). Fooled by Belligerence: Comments on Nassim Taleb's `The Long Peace is a Statistical Illusion'.
Richardson, L.F. (1948). Variation of the frequency of fatal quarrels with magnitude. Journal of the American Statistical Association, 43, 523-546.
Røsjø, B. (2018). Uvisst om Den lange freden er kommet for å bli. News article in titan.uio.no.
Schweder, T. and Hjort, N.L. (2016). Confidence, Likelihood, Probability. Statistical Inference With Confidence Distributions. Cambridge University Press.
Tolstoy, L.N. (1869). Война и мир. Русский вестник (the Russian Messenger).
Østerud, Ø. (2008). Towards a more peaceful world? A critical view. Conflict, Security & Development, 8, 223-240.

This particular FocuStat Blog Post rather quickly earned itself some extra fame, partly via Steven Pinker's twitter message: "Sophisticated new analysis of the stats of war by Nils Lid Hjort affirms a decline over time, but finds the sharpest in 1965, nor 1945." https://twitter.com/sapinker/status/952978002085892096 He was kind enough to write: "It’s a fascinating and sophisticated analysis, beautifully presented. It is interesting to consider 1965 as a possible breakpoint for a historical decline war. Certainly one finds mainstream attitudes changing around then, with an unprecedented (I think) antiwar movement; I suspect an analysis of cultural motifs (perhaps with Google ngrams) would show a transition starting around then." Another professor, who contributes regularly to the statistics and analyses of war-and-conflict data, wrote (to a colleague, not to me directly): "Thank you so much for sharing that link. That’s such a good article. Really informative and spectacularly well written (funny, clear, etc.) I really hope he takes it beyond a blog post. There is an important, publishable article in this." This attention has caused the Blog Post to be re-blogged here and there, etc. We at FocuStat are also seeing a bit of positive spill-over effect, that those reading the War-and-Peace blog then look at some of the others, etc.
Log in to comment
Not UiO or Feide account?
Create a WebID account to comment