Yes, the haul of metal and medals is pretty impressive, and it has demanded attention and forces for many of us, day after day, catching the most salient moments, living through the drama. For these strata of people this is not merely a nationalistic pastime, swimming in perceived passport-related glory, but a complex sociological process, where we also follow long lists of warm-hearted good-looking strong-willed competitors from other countries, with attention, admiration, and good wishes. In the Olympic Process of things I even went on tv and on radio and on Titan to explain the inner-outer intricacies of speedskating to The People, and to dicuss various other Olympic-sized Issues.

Molecular biologist Sigrid Bratli, Bioteknologirådet, and Nils Lid Hjort, FocuStat, discuss Eero Mäntyranta's wondrous triumphs on the 15 km and 30 km at the Innsbruck Olympics 1964 (where, as we recall, Harald Grønningen won the silvers), at Abels Tårn (Vaffel and Vitenskap to the People).
Sorting Metal and Counting Medals
Even though many of us have ecumenic and altruistic views, on our sofas, when watching the Olympics, part of the reason for getting up at 05:59 in the morning to watch the gruelling fifty-km cross-country race, minute by minute, remains, admittedly, hoping that Our Own do well. And, indeed, we [pluralis familiaris immodestiae et superbiae] did exceedingly well: 14 + 14 + 11 = 39 is a new Olympic Record (the USA had 9 + 15 + 13 = 37 in Vancouver, 2010). But there's an element of apples and pears here, or, rather, smaller and medium-sized and bigger apples. The number of events has increased drastically, from 16 in Chamonix, 1924, to 34 in Innsbruck, 1964, to a high 61 at Lillehammer and Hamar, 1994, to a whooping 102 at PyeongChang 2018. Surely, Thorleif Haug and Johan Grøttumsbråten and Oskar Olsen and Clas Thunberg ("Alone Against All of Norway") and Julius Skutnabb and Sonia Henie didn't quite see it coming, the unheavenly legion of new types of events, from snowboarding and halfpiping and moguls and team figure skating and massastarts (yes, that's Dutch) and mixed relays and autocorrelated biathlon events and big-air to curling for couples (married or not). Hence, winning 39 medals in 102 events (in 2018) is arguably less impressive than winning 17 medals in 16 events (in 1924).
A statistician can at least start counting, and putting up ratios; perhaps he or she can also model the outcomes to learn about patterns and trends and influential factors (and predict the future). The counting business is in terms of gold + silver + bronze medals, and the relevant ratios, from the current Norwegian perspective, are the percentages of Norwegian medals, from Olympics to Olympics. Thus, in 2018 we won 14 + 14 + 11 = 39 medals out of 102·3 = 306 medal chances (12.7%), which is less than winning 10 + 11 + 5 = 26 medals out of 61·3 = 183 medal chances (14.2%) in Lillehammer 1994. It is similarly less than 14 medals from 37 events (13.3%, Grenoble, 1968) and 15 medals of 34 events (14.7%, Innsbruck, 1964). And, amazingly, Norway won 35.4%, 35.7%, 23.8%, 29.4% of the medals in the first four Winter Olympics, as well as about a quarter of the medals on home ground in 1952; see the table below. So perhaps our 39 medals flown home from Korea isn't quite a national, or an Olympic, or a world record, after all.
A Binomial Process Approach to Medal Counting
In addition to staring transfixedly at the medals, and their numbers, which are being used for national political reasons and thrown into various debates (should Norway ever bother to host the Olympics again, for example, or is it easiest for us to come to lots of other parties, grab most of the medals and eat most of the food, party hard, and fly home), a statistician can sit back for a moment and contemplate the underlying processes, to check for trends, patterns, regime shifts, and assess the variability of podia. Here we may start by considering $\widehat p=y/(3m)$, for each Winter Olympics, the binomial proportion of $y$ medals won by Norway out of the $3m$ medal chances over $m$ events. I've plotted these percentages in the figure below, along with 90% confidence intervals. The horizontal blue line is the overall average of 11.6%, for winning 368 medals across 1054 events.

We learn that the 2018 national data point is sufficiently fabulous, by all means, but also that it isn't a Wondrous Outlier, compared to the level achieved and kept in reasonable balance since Kuppern Moe Maier Innsbruck 1964. Reading from the confidence intervals we are reminded of the Collective National Trauma of Calgary 1988 ("og så faller Geir Karlstad") and the Somewhat Painful Torino 2006 (Northug sitting at home!). Largely speaking, we're not in "alt lykkes for denne regjering" terrain; Norway seems able to catch around 10% of all medals, regardless of the colour of the government and the increasing number of pseudo-youth-ish Olympic events and even the number of skiing days at Bjørnholt.
Olympic Factors
So one overall reading of the figure above (and the table below) is that Norway manages to win approximately 10% of the medals, more or less consistently, from Innsbruck 1964 onwards (modulo a couple of national traumas). We may also attempt to throw in Other Olympic Factors, thought to be responsible for part of this level of success. In statistical terms, this translates to modelling and then analysing
$p(x_j)={\rm Pr}\{\hbox{Norway wins the medal}\,|\,x_j\}$,
for any of the $3m_j$ medal occasions in Olympics $j$, as a function of potential influential factors, or covariates, $x_j$. So which $x_j$ could be thrown to logistic regression models, of the type
$p(x_j)=\exp(a+b x_j)/\{1+\exp(a+bx_j)\}$,
with extra-binomial podia variability? Could there be alarm variables, which should make Norwegians tremble with pre-Olympic anxiety, predicting less than 10% medal grabbing at the next Olympic?
As a Tiny Nation, we pay attention when Other Countries bother to write anything about us. Indeed our existence has been noted during these Korean weeks, and not always benevolently. Swedish Dagens Nyheter says it's a matter of money, nationalism, and snow.

These are sensible covariates, indeed, and I've bothered enough to check whether $x_j={\rm GDP}_j$ plays any statistically visible role, the Gross Domestic Product through the years. The answer is a "no, but"; we can't see any influence on the $\widehat p_j$, though the importance of economics and resources and sports budgeting are very clearly present. The reason why we can't read off this influence for these simple medal table data is a combination of (a) this is valid for all other strong sports nations too, and (b) the competition is harder, with more nations and more participants. The answer to the simple counterfactual what-if question, how would Norway have done without all the resources, would be "far fewer medals", though this can't easily be proven. The same goes for the question of whether the low national budgets for basic cultural upbringing, in music and the arts, remain a success factor for good Olympic performance.
I've also looked at the very noticeable increase not only in the number of events, but the number of countries taking part, and the sheer number of participants. The first few Olympics had 16, 25, 17, 28 nations; from 1964 to 1980 about 35 nations took part; and now, after 67 nations at Lillehammer 1994, we're up to an astounding 92 countries in 2018. Again, like for the GDP numbers, we can't see any visible influence of these participation numbers on the medal grabbing probabilities $p_j$. The positive Norwegian spin on this is that our medal catching abilities have remained about constant, since 1964, despite harsher competition.
The Tiny Country's Tiny Secrets
Amazingly, even Big Media in other countries are writing about the Norwegian medal catching abilities, offering tentative explanations and speculative factors behind the heist (and, interestingly. with most of the headlines telling their readers that the articles give them The Norwegian Secrets, which means we need to develop New Secrets for the coming Olympics). You may check The Guardian's Norse Code theories (egalitarian society, the team experience, no jerks), TIME's crushing theories (working hard, let the children play, bosses not being gorillas, never asking a fellow human being how much she or he weighs, apparently), CNN's yet further secrets (winning by focusing on not focusing on winning, which sounds difficult, but we manage), etc.
Yes, there's something there, in these Revealed Secrets, which are of course not secrets but just plain facts of Norwegian habits, instincts, lives. There are a couple of other dimensions to point to. Yes, we still manage to be a decently egalitarian society, where we might bump into the king or the finance minister or Martine Ripsrud while skiing or in the bookshop and say "hei" and we don't weaponise our teachers and students. After all, we belong to The Almost Nearly Perfect People. These (remaining) egalitarian aspects are also reflected in how most of us look at sports. In various other societies, we learn by our anthropological tourist studies, there's somehow a bigger sociological distance between the top athletes and the mainstream people, and between the mainstreamers and say the top academics, than in Norway. Reading Schwaning and his fascinating Bildung. Alles, was man wissen muß, for example, teaches us what we're supposed to know, to have a good Bildung in life – but also, intriguingly, we're being told what we should rather not know ("Was man nicht wissen sollte"). We should rather not know about the personal records of Dutch and Soviet speedskaters from the 1960ies and 1970ies, and neither about Eggen vs. Tiainen and Vedenin, or Alsgaard vs. Teichmann, or Kulizhnikov vs. Murashov (I take it), since that's about as bad a stain on your personality as paying too much attention to sladreblader and die Regenbogepresse and paparazzi reports.
But we are different (apparently), and we dare to be. It's considered perfectly acceptable, even for the intellectuals and for academics, to take a serious interest in the sociology, history and current nerdy details of sports, and perhaps in the Winter Olympics sports and details in particular. Read Knausgård's heart-warming essay on the secrets of speedskating, read Thor Gotaas, read Eldar Høidal, read Rune Slagstad. Perhaps the Svenska Akademien and the rest of the literary world are utterly surprised and bewildered when they encounter forty pages of speedskating details in the middle of Dag Solstad's Nordisk Råds Litteraturpris winning novel. We're not.

Two of the many Norwegian 2018 gold medallists.
Norway, Germany, Canada are Equally Wondrous Countries
Chance plays a role in these games, of course (which might be why they're called games). Even Norwegians might admit that Håvard Holmefjord Lorentzen's 0.01 win over over Cha Min-kyu in the 500 m could have turned out the other way, and even the Dutch might nod to the thought that Lorentzen's 0.04 loss to Kjeld Nuis in the 1000 m is close to zero. Similarly, there were as usual a little string of dramatic half-traumatic fourth-places which very easily could have been bronzes. With this in mind we may have another look at the overall medal table, attempting to interpret the counts as statistical sightings of underlying hard-core probabilities, and then ask whether the probabilities
$p_{\rm NOR}$, $p_{GER}$, $p_{\rm CAN}$
are really that different:
\(\eqalign{ \qquad & &G &S &B \cr \qquad 1 &\hbox{Norway} &14 &14 &11 &\quad 39 \cr \qquad 2 &\hbox{Germany} &14 &10 & 7 &\quad 31 \cr \qquad 3 &\hbox{Canada} &11 & 8 &10 &\quad 29 \cr \qquad 4 &\hbox{Sambandsstatene}& 9 & 8 & 6 &\quad 23 \cr \qquad 5 &\hbox{Netherlands} & 8 & 6 & 6 &\quad 20 \cr \qquad 6 &\hbox{Russia} & 2 & 6 & 9 &\quad 17 \cr \qquad 7 &\hbox{South Korea} & 5 & 8 & 4 &\quad 17 \cr \qquad 8 &\hbox{Switzerland} & 5 & 6 & 4 &\quad 15 \cr \qquad 9 &\hbox{France} & 5 & 4 & 6 &\quad 15 \cr \qquad 10 &\hbox{Sweden} & 7 & 6 & 1 &\quad 14 \cr \qquad 11 &\hbox{Austria} & 5 & 3 & 6 &\quad 14 \cr \qquad 12 &\hbox{Japan} & 4 & 5 & 4 &\quad 13 \cr \qquad 13 &\hbox{Italy} & 3 & 2 & 5 &\quad 10 \cr}\)
So yes, even a statistician might admit that these metal counts 39, 31, 29 for the three top contenders Norway, Germany, Canada are different. But to what extent are they different – is it a mere matter of chance, where the Olympic Gods throw discuses and cast dies, deciding on the gold-silver-bronze games of the top nations? In statistical terms, are the probability estimates of 12.7% (NOR), 10.1% (GER), 9.5% (CAN) significantly different? The answer is "no"; the natural log-likelihood-difference test yields a far too low chi-squared of 1.865 on 2 degrees of freedom to doubt the hypothesis that the three medal winning probabilities are different. This is also reflected in the confidence curves in the figure below. There is clear overlap for e.g. the 90% confidence intervals.
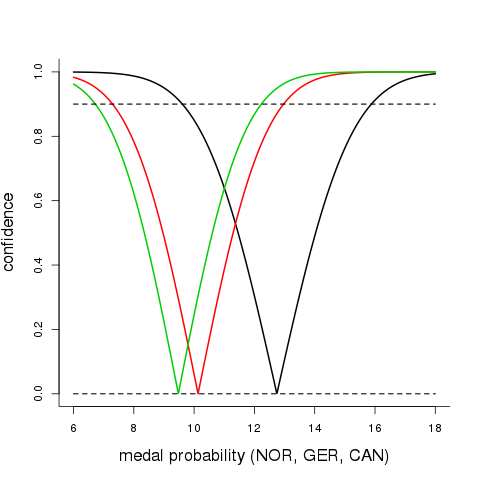
We learn from this little modesty exercise that Norwegians and specifically the Gro Harlem Brundtlands amongst us need to lower their bragging parameters a bit; it's just by chance (or, at least, partly by chance; dans les champs de l'observation le hasard ne favorise que les esprits préparés, says Pasteur), that we "won" over Germany and Canada, this time. In Beijin 2022 or at Geilo 2030, things might pan out differently, even if we're in principle just as good as the other top nations.
The Norwegian Medal Table, 1924 to 2018
The table gives for each Olympics the number of events, then the metal count (with total), followed by the number of nations taking part, and the percent of medals won by Norwegian athletes.
\(\eqalign{ \def\ha{\phantom{2}} \def\hb{\quad} \def\hc{\quad} & &{\rm events}&\hc G & S & B &{\rm total} &{\rm nations} &{\rm percent}\cr \hbox{ Chamonix } &1924 &\quad 16 &\hc 4 & 7 & 6 & 17 & \hb 16 &\quad 35.4 \cr \hbox{ St Moritz } &1928 &\quad 14 &\hc 6 & 4 & 5 & 15 & \hb 25 &\quad 35.7 \cr \hbox{ Lake Placid } &1932 &\quad 14 &\hc 3 & 4 & 3 & 10 & \hb 17 &\quad 23.8 \cr \hbox{ Garmisch } &1936 &\quad 17 &\hc 7 & 5 & 3 & 15 & \hb 28 &\quad 29.4 \cr \hbox{ St Moritz } &1948 &\quad 22 &\hc 4 & 3 & 3 & 10 & \hb 28 &\quad 15.2 \cr \hbox{ Oslo } &1952 &\quad 22 &\hc 7 & 3 & 6 & 16 & \hb 30 &\quad 24.2 \cr \hbox{ Cortina } &1956 &\quad 24 &\hc 2 & 1 & 1 & 4 & \hb 32 &\quad {\ha}5.6 \cr \hbox{ Squaw Valley } &1960 &\quad 27 &\hc 3 & 3 & 0 & 6 & \hb 30 &\quad {\ha}7.4 \cr \hbox{ Innsbruck } &1964 &\quad 34 &\hc 3 & 6 & 6 & 15 & \hb 36 &\quad 14.7 \cr \hbox{ Grenoble } &1968 &\quad 35 &\hc 6 & 6 & 2 & 14 & \hb 37 &\quad 13.3 \cr \hbox{ Sapporo } &1972 &\quad 35 &\hc 2 & 5 & 5 & 12 & \hb 35 &\quad 11.4 \cr \hbox{ Innsbruck } &1976 &\quad 37 &\hc 3 & 3 & 1 & 7 & \hb 37 &\quad {\ha}6.3 \cr \hbox{ Lake Placid } &1980 &\quad 38 &\hc 1 & 3 & 6 & 10 & \hb 37 &\quad {\ha}8.8 \cr \hbox{ Sarajevo } &1984 &\quad 39 &\hc 3 & 2 & 4 & 9 & \hb 49 &\quad {\ha}7.7 \cr \hbox{ Calgary} &1988 &\quad 46 &\hc 0 & 3 & 2 & 5 & \hb 57 &\quad {\ha}3.6 \cr \hbox{ Albertville } &1992 &\quad 57 &\hc 9 & 6 & 5 & 20 & \hb 64 &\quad 11.7 \cr \hbox{ Lillehammer } &1994 &\quad 61 &\hc 10 & 11 & 5 & 26 & \hb 67 &\quad 14.2 \cr \hbox{ Nagano } &1998 &\quad 68 &\hc 10 & 10 & 6 & 25 & \hb 72 &\quad 12.3 \cr \hbox{ Salt Lake City } &2002 &\quad 78 &\hc 13 & 5 & 7 & 25 & \hb 78 &\quad 10.7 \cr \hbox{ Torino } &2006 &\quad 84 &\hc 2 & 8 & 9 & 19 & \hb 80 &\quad {\ha}7.5 \cr \hbox{ Vancouver } &2010 &\quad 86 &\hc 9 & 8 & 6 & 23 & \hb 82 &\quad {\ha}8.9 \cr \hbox{ Sochi } &2014 &\quad 98 &\hc 11 & 5 & 10 & 26 & \hb 88 &\quad {\ha}8.8 \cr \hbox{ PyeongChang } &2018 &\quad 102 &\hc 14 & 14 & 11 & 39 & \hb 92 &\quad 12.7 \cr}\)
Other Olympic Perspectives and Tables
I suppose I've managed to flag my above-average interest in the Winter Olympics and the accompanying host of correlated issues and themes. Here are just a few further statistics related topics worthy of over-coffee conversations (along with what in academia is called "further thought").
A. This has clearly been the Worst Ever Winter Olympics for Norway. The number of events where we didn't win a single medal has never been so high. Checking golds only shows that we won a mere 14 golds in 102 events, which means 88/102 = 86.3% non-NOR-golds. In 1924 there were 12/16 = 75.0% non-NOR-golds. This doesn't go quite as far as "everything can be proven by statistics" or to Twain's front door of all the Lies, Damned Lies, and Statistics we can hurl in the general Olympic direction of things, but is a neutral reminder that we ought to concentrate our statistical efforts (counting, tableing, analysing, relating, comparing, modelling, predicting) on the more vital questions, as driven by context.
B. I'm not particularly fond of the incessant focus on the Medals and Only the Medals, however, and dislike the implied and often explicit notion of The Horrible Painful For Ever Embarrassing fourth place ("den sure fjerdeplassen" has about ten thousand google hits). There should be a special Norwegian Wood Medal for the exceedingly honorable 4th place, and I humbly ask the United Nations to see to it that this is institutionalised within the 2022 Beijin Olympics. At any rate, we can count them!, and my possible favourite, qua statistical long-term Olympic summary, is the notion of Olympic Points: 7-5-4-3-2-1 for gold-silver-bronze-4-5-6. Here's the top-six part of the full list, which can be found here, thanks to Erik Helmersen's diligent efforts.
\(\eqalign{ \qquad 1 &\hbox{Norway} &265.50 \cr \qquad 2 &\hbox{Germany} &221.25 \cr \qquad 3 &\hbox{Canada} &202.00 \cr \qquad 4 &\hbox{Sambandsstatene} &200.50 \cr \qquad 5 &\hbox{Netherlands} &123.00 \cr \qquad 6 &\hbox{France} &118.00 \cr}\)
C. Rather than counting medals for absolutely all of the events (including what is sometimes called "circus events"), one may of course form separate medal tables for the core long-standing events. I'm tempted to spend some evening half hours disentangling tables such as the following, to look for potential trends over years, etc. It gives the number of medals, for men, for ladies, and combined, for speedskating events, from 1924 to 2018 (ladies, the word consistently used by the International Skating Union, were allowed only from 1960 onwards). So for at least four more years, NOR is still ahead of NED on the list, when it comes to the men's gold medals. I haven't pursued this here, however.
\(\eqalign{ \qquad &\hbox{Netherlands} &76 &45 &\quad 121 \cr \qquad &\hbox{Norway} &82 & 2 &\quad 84 \cr \qquad &\hbox{USA} &40 &28 &\quad 68\cr \qquad &\hbox{CCCP} &31 &29 &\quad 60\cr \qquad &\hbox{Germany} & 3 &35 &\quad 38 \cr \qquad &\hbox{Canada} &18 &19 &\quad 37\cr \qquad &\hbox{DDR} & 5 &24 &\quad 29\cr \qquad &\hbox{Finland} &19 & 5 &\quad 24\cr \qquad &\hbox{Japan} &11 &10 &\quad 21\cr \qquad &\hbox{Sweden} &16 & 0 &\quad 16\cr \qquad &\hbox{Korea} &12 & 4 &\quad 16\cr \qquad &\hbox{Russia} & 6 & 7 &\quad 13 \cr}\)
D. We're a Tiny Nation, with a healthy production of metal per capita, but we're being Olympically soundly outperformed by Liechtenstein, in the medal-per-capita event:
\(\eqalign{ \qquad 1 &\hbox{ Liechtenstein } &\phantom{3}1 &\quad 37,531 &\quad 37,531 \cr \qquad 2 &\hbox{ Norway } &39 &\quad 5,195,921 &\quad 133,228 \cr \qquad 3 &\hbox{ Switzerland } &15 &\quad 8,286,976 &\quad 552,465 \cr \qquad 4 &\hbox{ Austria } &14 &\quad 8,611,088 &\quad 615,077 \cr \qquad 5 &\hbox{ Sweden } &14 &\quad 9,798,871 &\quad 699,919 \cr \qquad 6 &\hbox{ Netherlands } &20 &\quad 16,936,520 &\quad 846,826 \cr \qquad &\ldots \cr \qquad 14 &\hbox{ Germany } &31 &\quad 81,413,145 &\quad 2,626,230 \cr \qquad 15 &\hbox{ South Korea } &17 &\quad 50,617,045 &\quad 2,977,473 \cr} \)
Tina Weirather (who also has an Austrian citizenship) won a bronze in the ladies' Super-G, and hence singlehandedly, or singleskiedly, won against all of Norway. It turns out that 70% of all Olympic medallists from Liechtenstein come from the same family, so the simplest thing to do for Norway would perhaps be to offer them all asylum (complete with a range of the famous Norwegian well-fare benefits). For various other fascinating lists, for per-capita, per-area, per-GDP, per-latitude (!), etc., check the medals-per-capita page.
Thanks
I'm grateful to all the 2922 participants in the 2018 Olympics – and, by backwards induction, to the participants of all previous Winter Olympics (from the 2800 in Sochi 2014, to the 1738 in Lillehammer and Hamar 1994, the 1094 in Innsbruck 1964, the 494 in Oslo 1952, and the 292 in Chamonix 1924). I also appreciate that science journalists and NRK apparently read our FocuStat Blog Posts, with my 2 x 1000 m piece leading to apperances in Abels Tårn (where I was properly starstrøkked) and in Titan. I thank Céline Cunen and Helge Julius Jakhelln Dyvik for useful comments. Finally, a vigorous nod ought to be given to the stimulating and variegated contributions from flocks of eager people in the Forum for Skøyehistorie at Facebook, where we watch and comment and discuss and shout and sigh (and disagree) on a day-by-day basis during the bigger championships.
References
Booth, M. (2014). The Almost Nearly Perfect People. Jonathan Cape, Vinstra.
CNN (February 2018). The secret behind Norway's Winter Olympic success.
Gotaas, T. (2015). Femmila. Skisportens manndomsprøve. Gyldendal, Brumunddal.
Guardian (February 2018). Norse code: what’s the secret of the Norwegians’ Winter Olympics success? Hailing from a nation of only 5.2 million people, Norway’s squad is outperforming teams from much bigger countries – and, no, it’s not just because they have so much snow.
Gundersen, J.-A.Ø. (2018). Redningsskøytene. 12-page report and essay on the new wave of Norwegian top skaters, in Dagens Nærlingslivs D2 magasin.
Hjort, N.L. (1994). Should the Olympic speedskaters race the 500 m twice? Statistical Research Report, Department of Mathematics, University of Oslo. (Yes, this report changed the Olympics.)
Hjort, N.L. (2017). But some are more equal than others. FocuStat Blog Post.
Hjort, N.L. (2017). The semifinals factor for skiing fast in the finals. FocuStat Blog Post.
Hjort, N.L. (2018). One Thousand is Unfair, Two Thousand is Fair. FocuStat Blog Post.
Høidal, E. (2012). To indre og vekk me'n. Cappelen-Damm, Oso.
Knausgård, K.O. (2018). The Hidden Drama of Speedskating. Essay, The New York Times, 1-Feb-2018.
Rosa, D. and Hjort, N.L. (1999). Who Won? The Annual Speedskating Race of the Burg of Ducks. Speedskating World. (Also included in Don Rosa Collected Works, 2011.)
Schwanitz, D. (1999). Alles, was man wissen muß. Eichborn, Frankfurt am Main.
Solstad, D. (1989). Roman 1987. Oktober, Sandefjord.
Slagstad, R. (2008). (Sporten) En idéhistorisk studie. Pax, Oslo.
TIME Magazine (February 2018): Norway Crushed the Competition at the Winter Olympics. Here Is the Tiny Country's Secret.


Log in to comment
Not UiO or Feide account?
Create a WebID account to comment