The six finalists have gone through a gruelling sequence of prologue, quarterfinals, semifinals, each demanding top manouevring skills and split-second tactical decisions, at barely imaginable speeds of 30 km/hour and more, over about 1.5 km distances in highly varying terrain. With A and B denoting the first and the second of the semifinals, these are the results from the Sochi 2014 Olympics:
| 1 | O.V. Hattestad | A | 1 | M.C. Falla | A |
|---|---|---|---|---|---|
| 2 | T. Peterson | A | 2 | I.F. Østberg | B |
| 3 | E. Jönsson | B | 3 | V. Fabjan | A |
| 4 | A. Gløersen | A | 4 | A.U. Jacobsen | A |
| 5 | S. Ustiugov | B | 5 | I. Ingemarsdotter | A |
| 6 | M. Hellner | A | 6 | S. Caldwell | B |
So the A skiers (and the Norwegian gold medallists) apparently do a bit better than the B skiers ... is this merely by chance?
Not even a statistician can make any claims that something systematic is taking place here, based on the results from a single event. But with such result tables from a decent number of ski sprint events, I can make a proper analysis, and assess whether any differences between A skiers and B skiers are due to randomness, or whether there is a half-hidden structural factor at work.
I've collected together such result tables, for a total of 57 ski sprint events \(-\) Olymic games, World Championships, World Cup events, and for each occasion checking how the As (first semifinal) and the Bs (second semifinal) turn up for the top-6 lists of the finals. Finding my 57 tables involved using ths FIS site (for seasons 2014, 2013, 2012, and involving a bit of manual fiddling), wikipedia pages, and pestering a FIS secretary in Lausanne for results also from 2011, 2010. The point is then to work with
Problem One: Is there a difference at all, regarding these outcomes, or are we merely looking at a lottery type randomness (which is what the skiers and the IOC and the FIS should hope for)?
Problem Two: If there is a difference (and, surprise or not, the answer is yes!), how much does it matter, on the Olympic scale of fairness?
I approach these problems by setting up a probability model structure for the data, involving certain parameters. Problem One is that of testing the statistical null hypothesis \(H_0\), in terms of these parameters, that there is zero difference between A and B. Problem Two is to translate data information via the model parameters into relevant estimates of unfairness, e.g. by estimating
p = Pr(the winner is an A skier).
So, if you have 3 red and 3 blue socks in your drawer, and you blindfoldedly draw these one-by-one each morning, the question is: To what degree do you need to see red socks tending to appear earlier than the blue socks, and for how long, before you can feel statistically certain that something's going on?
I'm looking at the ranks \(-\)for Sochi 2014, we have A A B A B A for the men and A B A A A B for the ladies. (The two best from each semifinal go to the final, along with the two Lucky Losers with the best times; thus we may have 4 A + 2 B, or 3 A + 3 B, or 2 A + 4 B.) I form the rank sums
\(Z_A=\sum_i X_i \quad{\rm and}\quad Z_B=\sum_j Y_j,\)
where \(X_i\) are the rank positions for A skiers and \(Y_j\) the rank positions for B skiers. For the Sochi results,
\(\eqalign{ Z_A=1+2+4+6=13 \quad{\rm and}\quad Z_B=3+5=8, \cr Z_A=1+3+4+5=13 \quad{\rm and}\quad Z_B=2+6=8.\cr}\)
The sum is 21 regardless, so it suffices to examine the \(Z_A\). My test statistic is the combined rank sum
\(Z=\sum_{j=1}^{57} Z_{A,j}=\sum_{{\rm two\ A}}Z_{A,j}+\sum_{{\rm three\ A}}Z_{A,j}+\sum_{{\rm four\ A}}Z_{A,j},\)
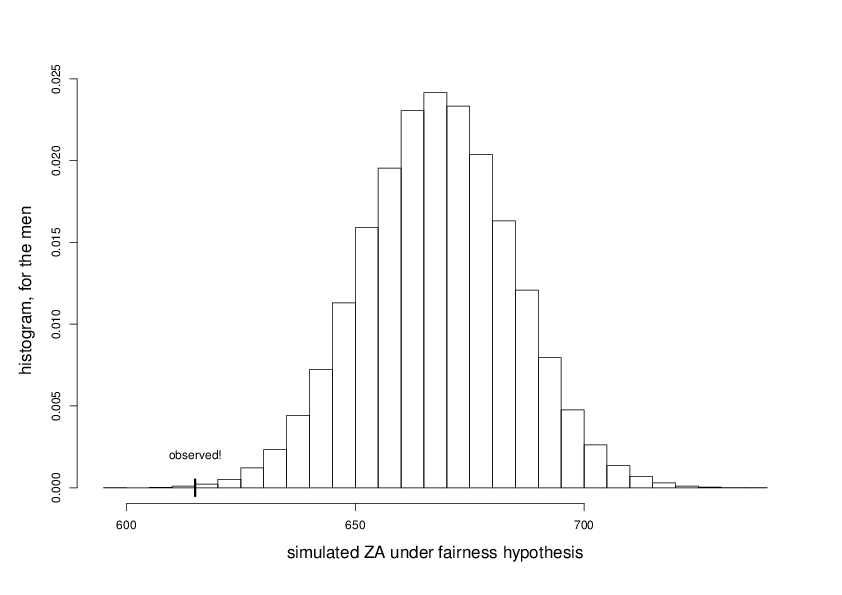
summed over all 57 events, but separately for men and women. I then check whether the observed values are probable, or not at all, under the null hypothesis. For men, I find \(Z_A=615\), which is far too low, when judged from the null hyothesis of A and B skiers having the same chances (p-value 0.0006). This is seen in the figure, with the observed 615 marked against the distribution of such \(Z_A\) drawn under the condition of fairness. So Conclusion One is that there's a serious advantage for the A skiers, those coming from the first semifinal: they tend, in a crystal clear statistical sense, over time, to have better ranks, to be more often on the podium, than the B skiers.
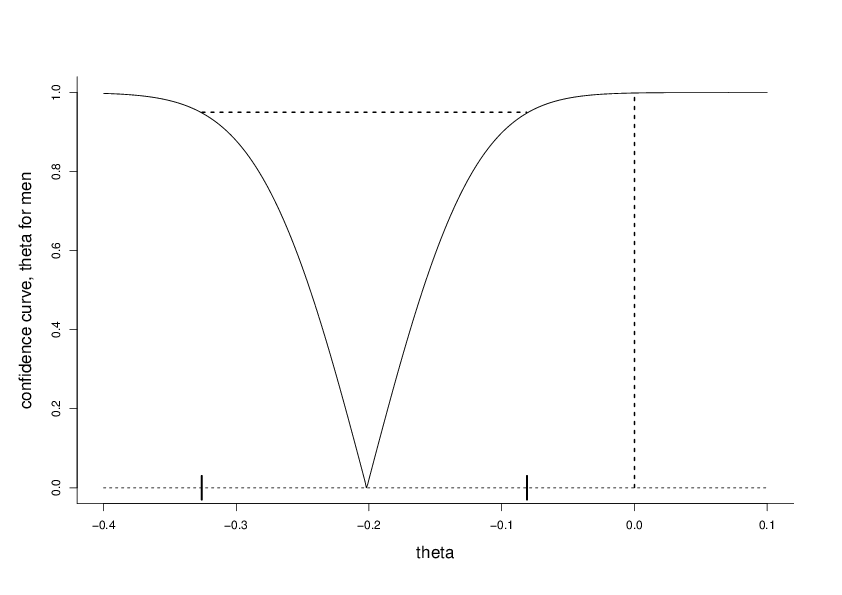
Conclusion One, though already important, does not yet help us understand to what extent the Olympic setup is unfair. To assess this we need a probability model, then to be fitted using the data. My model takes
\(\eqalign{ f_{24}(i,j,\theta)&=e^{\theta(i+j)}/K_{24}(\theta), \cr f_{33}(i,j,k,\theta)&=e^{\theta(i+j+k)}/K_{33}(\theta), \cr f_{42}(i,j,k,\theta)&=e^{\theta(i+j+k+l)}/K_{42}(\theta), \cr}\)
with \(K_{22}(\theta)\) a sum over all 15 terms for picking two results for two A skiers, and similarly for \(K_{33}(\theta)\) and \(K_{42}(\theta)\), with respectively 20 and 15 terms. If the \(\theta\) parameter is zero, the world is fair; but here we learn, through a confidence distribution analysis, that it is clearly negative, implying that A skiers have a serious advantage over B skiers.
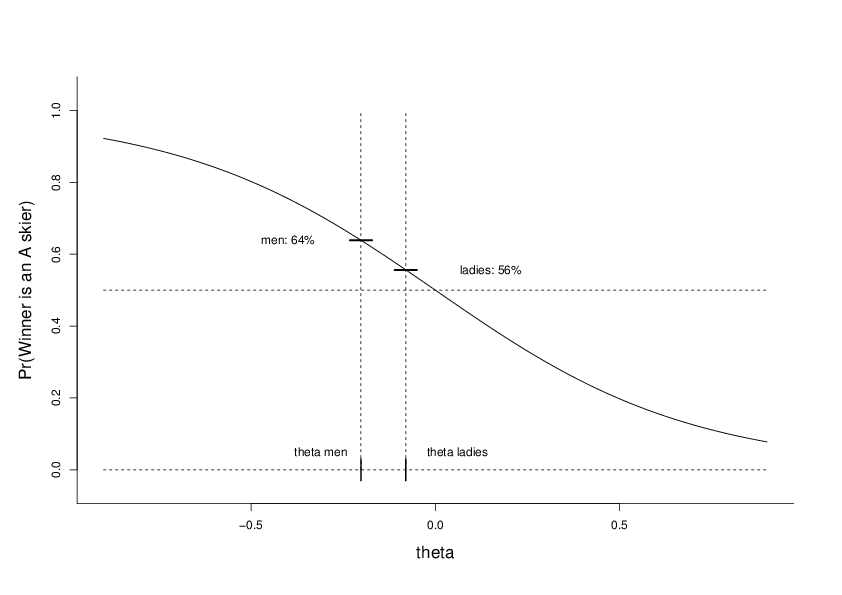
The model may also be used to see just how unfair the world is (well, up to now, see below). The figure below, arrived at via calculations using the parametric model, shows that there is a 64% chance that the winner is an A skier, 36% chance that it is a B skier.
Interestingly, the findings above, which have been communicated to the Fédération Internationale de Ski (FIS) up to the Vegard Ulvang level of Big Decision Makers in the world (I worked with Øyvind Sandbakk at Olympiatoppen on this), are at the outset purely statistical, without so far going into likely reasons for the differences we're seeing here. There is an explanation, however, related to the amount of extra recuperation time the A skiers have, compared to the more time-troubled B skiers. Thus Nikita Kriukov and Aleksandr Panzhinskiy were rather more rested, before the Vancouver 2010 final, than e.g. poor Northug, who had worked extremely hard to earn his place in the final just few minutes earlier. For the Sochi 2014 final, gold-winner Hattestad had 20 minutes rest, Ustiugov merely 13 minutes.
Blood lactate measurements of athletes have been undertaken to assess these physiological processes (along with other analyses), and a rough estimate is that top athletes need at least twenty minutes of relative rest, before being fit enough again to work Olympically hard for another gruelling three minutes of cross-country ski sprinting.
The solution, from the FIS practical point of view, is to make sure that also the B skiers from the 2nd semifinal have enough recuperation time, even if it takes Justin Bieber or Leiv Ove Andsnes being flown in to keep the zillions of television viewers hooked for a few extra minutes while the athletes breathe. Work summarised here, with more detail in Schweder and Hjort's CLP book (Section 8.8), contributed to these decisions and practical rearrangements, from the 2015-2016 winter season onwards.
P.S. This blog post was written on the day where Maiken Falla, Jessica Diggins, Kikkan Randalph, Frederico Pellegrino, Сергей Устюгов, Johannes Høsflot Klæbo won their ski sprint medals in the Lahti 2017 World Championships.
References:
Schweder, T. and Hjort, N.L. (2016): Confidence, Likelihood, Probability: Statistical Inference With Confidence Distributions.
Hjort, N.L. (1994). How I changed the Olympics (well, regarding a different event).

1. The FIS didn't follow its own intentions and regulations, for the 23-Feb-2017 Lahti World Championships ski sprint event. Semi-1 skiers had 24:30 minutes, semi-2 skiers only 15:30 minutes, until the finals started. As far as I've understood, FIS has agreed on 20:00 minutes for all, after the work reported on above. As we may see, the semi-1 skiers did best: A A A B A B (poor Finn Hågen Krogh) 2. Above I wrote: " The solution, from the FIS practical point of view, is to make sure that also the B skiers from the 2nd semifinal have enough recuperation time, even if it takes Justin Bieber or Leiv Ove Andsnes being flown in to keep the zillions of television viewers hooked for a few extra minutes while the athletes breathe. " I've not yet heard from J. Bieber, but Leiv Ove Andsnes comments (on Facebook): Leif Ove Andsnes - privat Du verden! Like · Reply · 1 · 17 mins
Log in to comment
Not UiO or Feide account?
Create a WebID account to comment