Markovkjeder har mange praktiske anvendelsesområder. Markovkjeder Monte Carlo (MCMC) er stokastiske simuleringsmetoder for å analysere komplese sannsynlighetsfordelinger, brukt blant annet i Bayesiansk statistikk. Sannsynligheten for at et system er i et spesielt stadium ved tid t avhenger bare av stadiet til systemet ved tiden t-1, og avhenger ikke av hva som var før t-1. Finnes som tostadiemodeller og multistadiemodeller. Det er rransisjonssannynlighetsmatriser (stokastiske matriser) for bevegelse mellom to stadier. Markov-matriser M er kvadratmatriser
Sannsynlighetene p i en rad i transisjonsmatrisen blir lik 1 i sum.
\(\displaystyle M = \begin{pmatrix} p_{1,1} & p_{1,2} & \cdots & p_{1,n} \\ p_{2,1} & p_{2,2} & \cdots & p_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ p_{n,1} & p_{n,2} & \cdots & p_{n,n} \end{pmatrix}\)
Metropolis-Hastings algoritmen er et eksmpel på en MCMC-metode , navn etter den grask-amerikanske fysikeren Nicholas Metropolis (1915-1999), utvidet av Wilfred Keith Hastings (1930-2016). En kjent sannsynlighetsfordeling angir neste punkt i virrevandinrgen ("random walk"). Ved Los Alamos utarbeidet Metropolis, sammen med John von Neumann og Stanislaw Ulam, Monte Carlo-teknikken basert på slumptall. Metropolisalgoritmen ble brukt i simuleringen av Ulam-Teller hydrogenbomben, og den virket som i simuleringen. Verden ble ikke den samme som før.
Gibbs sampler, navn etter den amerikanske fysikeren Josiah Willard Gibbs (1839-1903) er en MCMC-algoritme brukt til å hente data som er beskrevet av en multivariat sannsynlighetsfordeling, anvendt blant annet innen Bayesiansk inferens. Sammen med Ludwig Boltzmann og James Clerk Maxwell utviklet Gibbs fagområdet statistisk mekanikk.
Markovkjeder er en tidsavhengig stokastisk prosess. Tidsindeksen har positive heltall. Prosessen starter ved stadium X0 og fortsetter med transisjoner til X1, X2,…, Xt,…
Hvis tidrommet er endelig kan sannsynligheten for et stadium til det neste beskrives av en transisjonsmatrise. MCMC er Markovkjede Monte Carlometoder.
Anta at man starter på et punkt på sirkelen nedenfor, for eksempel 5, og det er like sannsynlig at man blir stående som å bevege seg til en av sidene. Det er ingen hukommelse i dette hvor man har vært tidligere. Man bruker en transisjonsmatrise med sannsynligheter til å beskrive prosessen.
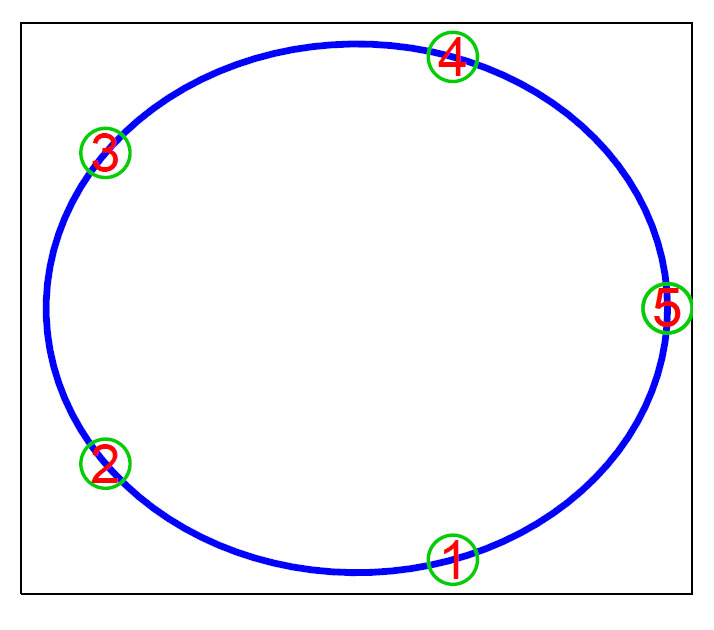
En transisjonsmatrise viser sannsynlighetene, hvor første rad er sannsynligheten for å flytte seg i et enkelt trinn fra lokalitet. Neste linje er for lokalitet 2 osv.. Summen av radene og kolonnene i transisjonsmatrisen blir lik 1.
Eksempel 2
Her er eksempel på en Markov-kjede med 4 tilstander som bare kan nås i en retning er en periodisk kjede hvor perioden er lik 4. Den konvergerer ikke. Hvis man starter ved A ved t=0 er man tilbake til A ved t=4, 8, 12,…

Eksempel 2
Eksempel på en Markov-kjede er en organisme som har to lokaliteter eller habitater A og B hvor man noterer for hver tidsenhet om organismen befinner seg på lokalitet A eller B. Sannsynligheten for at organismen beveger seg fra den ene lokaliteten til den andre eller (A til B, B til A) fortsetter å være på lokaliteten er angitt på figuren (A til A, B til B). Vi starter med organismen på lokalitet A ved t=0.
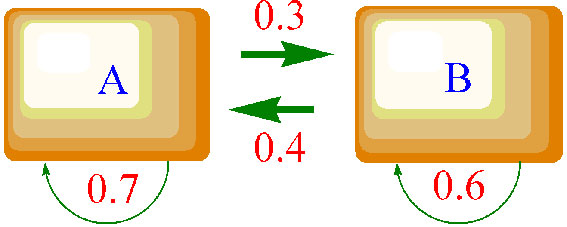
Vi kan nå lage en transisjonsmatrise for startbetingelsene hvor raden er startlokalitet og kolonnene er endelokaliteten for hver bevegelse. Vi lar hendelsene med flytting av lokalitet være uavhengig av hverandre.
Transisjonsmatrise M:
\(M= \begin{pmatrix} 0.7 & 0.3\\ 0.4 & 0.6 \end{pmatrix}\)
Ved gejntatt matrisemultiplisering med transisjonsmatrisen vil kjeden konvergerer og når en stasjonær tilstand og transisjonsmatrisen endrer seg ikke lenger. Ender med samme sannsynlighet 0.57 for å gå fra A til A som fra B til A, og 0.43 sannsynlighet for B til B og A til B.