Normalfordelingskurven (klokkekurven, Gausskurven) for en stokastisk (varierer tilfeldig) variabel er bare bestemt av forventet verdi, E(X)= gjennomsnittsverdien (µ)) og varians (Var(X)=σ2).
Vi bruker stor X for å angi en stokastisk (tilfeldig) variabel og x1,x2,x3,…,xn for å angi de enkelte måleverdiene til variabelen. Mengden av verdiene til den stokastiske variabel X utgjør en verdimengde.
Standardavviket (σ) er lik kvadratroten av varians. Siden varians er summen av kvadrerte avvik dividert på n (eller n-1 hvis det er en prøve) så får varians måleneht kvadratet av måleenheten. Derfor er standardavviket kvadratroten av varians slik at man kan angi et spredningsmål for eksempel gjennomsnittsverdi pluss/minus et standardavvik med samme måleenhet.
Normalfordelingskurven
Den stokastiske variabelen X er modellert av av den kontinuerlige normalfordelingsfunksjonen N med gjennomsnitt (μ) og varians (σ2).
\(X \sim N(\mu, \sigma ^2)\)
Totalarealet under normalfordelingskurven er lik 1. Funksjonen f(x) kalles sannsynlighetstetthetsfunksjonen og beskriver sannsynlighetsfordelingen for en kontinuerlig tilfeldig normalfordelt variabel.
\(f(x)= \displaystyle\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{X- \mu}{\sigma}\right)^2 }\)
Enhver funksjon f(x) kalles en sannsynlighetstetthetsfunksjon hvis:
\(f(x) \geq 0 \;\; \text{for }\;\; a \leq x \leq b\)
og
\(\displaystyle \int_a^b f(x) dx = 1\)
For normalfordelingskurven er a lik minus uendelig, og b er pluss uendelig, det vil si at halene på normalfordelingskurven aldri kommer helt ned til x-aksen, den nærmer seg bare asymptotisk.
Det betyr at funksjonen mellom grensene a og b må ligge over x-aksen og at totalt areal under kurven i det samme området er lik 1=100%.

Forskjellige normalfordelingskurver N(μ,σ2)) (sannsynlighetstetthetfunksjoner), med en gjennomsnittsverdi μ= 2 og med forskjellig standardavvik (σ) = (kvadratrot av varians). Etterhvert som standardavviket øker så øker bredden på kurven og høyden minker. Sannsynlighetstetthetsfunksjonen for normalfordelingen kalles også klokkekurven på grunn av formen, eller Gausskurven oppkalt etter matematikeren Gauss. Normalfordelingskurven nærmer seg asymptotisk mot x-aksen og går fra minus uendelig (-∞) til pluss uendelig (∞). Toppen av kurven er ved x = μ og høyden av toppen er lik :
\(\displaystyle\frac{1}{\sigma \sqrt{2\pi}}\)
Legg merke til at tallet pi inngår i ligningen for normalfordelingen.

Kumulativ fordelingsfunksjon
Fordelingsfunksjonen F (x) for normalfordelingen er lik integralet av sannsynlighetstetthetsfunksjonen f(x).
\(F(x)= \displaystyle\frac{1}{\sigma \sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{1}{2}\left(\frac{X- \mu}{\sigma}\right)^2 }dx\)
\(F(x) \rightarrow 1 \;\; \text{når}\;\; x\rightarrow \infty\; \text{(uendelig)}\)
Integralet av sannsynlighetstetthetfunksjonen f(x) fra minus uendelig (-∞) til pluss uendelig (∞) er lik 1, og siden sannsynligheter går fra 0 til 1, kan man bruke deler av arealet under f(x) til å beskrive sannsynligheter, og det gjør man med den kumulative fordelingsfunksjonen F(x).
Normalfordelingen ble først oppdaget av den franske matematikeren Abraham de Moivre som også kunne vise at den binomiale fordelingen konvergerer mot normalfordelingen, et resultat av sentralgrenseteoremet. de Moivre oppdaget også Stirlings formel.
Normalfordelingen har en rekke nyttige egenskaper. Hvis man har to uavhengige normalfordelte tilfeldige variable X og Y så er summen av dem også en normalfordelt variabel med forventet verdi E(X+Y)=E(X)+E(Y) og Var(X+Y)=Var(X)+Var(Y).
Poisson-, binomial-, negativ binomial- og gamma-fordelingen for diskrete variable kan under gitte betingelser følge normalfordeling.
Standard normalfordeling
Normalfordelingen lett flyttes og skaleres. En slik skalering brukes når man lager standard normalfordeling N(0,1) hvor hvor gjennomsnittet er lik null (μ=0) og standardavviket er lik e σ=1.
Sannsynlighetstetthetsfunksjonen for standard normalfordeling blir:
\(f(z)=\displaystyle\frac{1}{2\pi}e^{-\frac{z^2}{2}}\;\;\;\;\;\, -\infty<z<\infty\)
Kumulativ sannsynlighetsfordelingsfunksjonen F(z) er gitt ved:
\(F(z)=\displaystyle\frac{1}{2\pi}\int _{-\infty}^ze^{-\frac{z^2}{2}} dz= Pr(Z\leq z)\)
og det er denne fordelingen man finner i statistiske tabeller og viser arealet under standardnormalingsfunksjonen i intervallet [-∞, z], altså til venstre for z.
z-skår er antall standardavvik(σ)som en verdi er vekk fra gjennomsnittet:
\(z=\displaystyle\frac{x-\mu}{\sigma}\;\;\;\;\;\;\; \;\; \,\; x= \mu + z\sigma\)
For standard normalfordeling blir E(z) = 0 og Var(z) = 1.
Hvis vi har en tilfeldig variabel X som er normalfordelt med gjennomsnitt µ=2 og standardavvik σ=0.5, så blir z=(X-2)/0.5 fordelt etter standard normalfordeling med gjennomsnitt=0 og standardavvik=1.
Hva er sannsynligheten for at en slik variabel befinner seg i intervallet Pr{1.6 ≤ X≤ 2.4} ? Vi regner om til z-skår og finner det tilsvarende areal under standard normalfordeling, i dette eksemplet tilsvarer det 57.6% sannsynlig.
Sannsynlighetstetthetsfordelingen f(x) for en standard normalfordeling har formel:
\(f(x)=\displaystyle\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\;\;\;\;\;\, -\infty<x<\infty\)
Den kumulative sannsynlighetsfordelingen F(x) for en standard normalfordeling:
\(F(x)= \displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{-{\frac{x^2}{2}} }dx\)
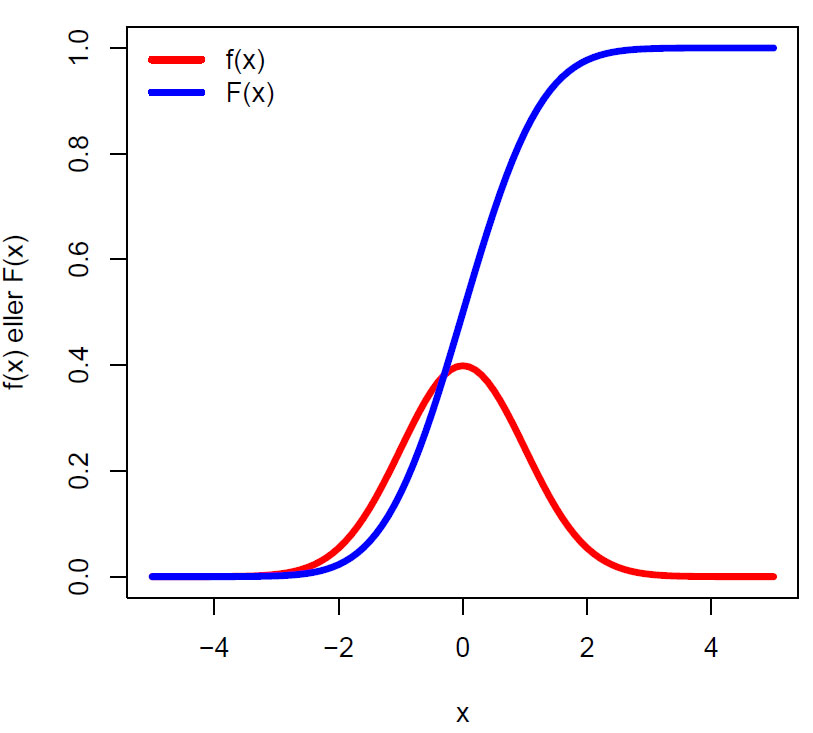
Sannsynlighetstetthetskurven f(x) (rød kurve) gir ikke et mål på sannsynlighet, men det gjør F(x) (blå kurve) som omfatter området [0,1] og er lik det kumulative integralet av f(x). Standard normalfordeling har gjennomsnittsverdi for populasjonen µ = 0 og standardavvik for populasjonen σ = 1. Vi bruker de greske bokstavene når vi snakker om populasjonen. Legg merke til at gjennomsnittet (μ=0) og maksimumspunktet for f(x) er lik:
\(\displaystyle\frac{1}{\sqrt{2\pi}}= 0.3989423 \dots\)
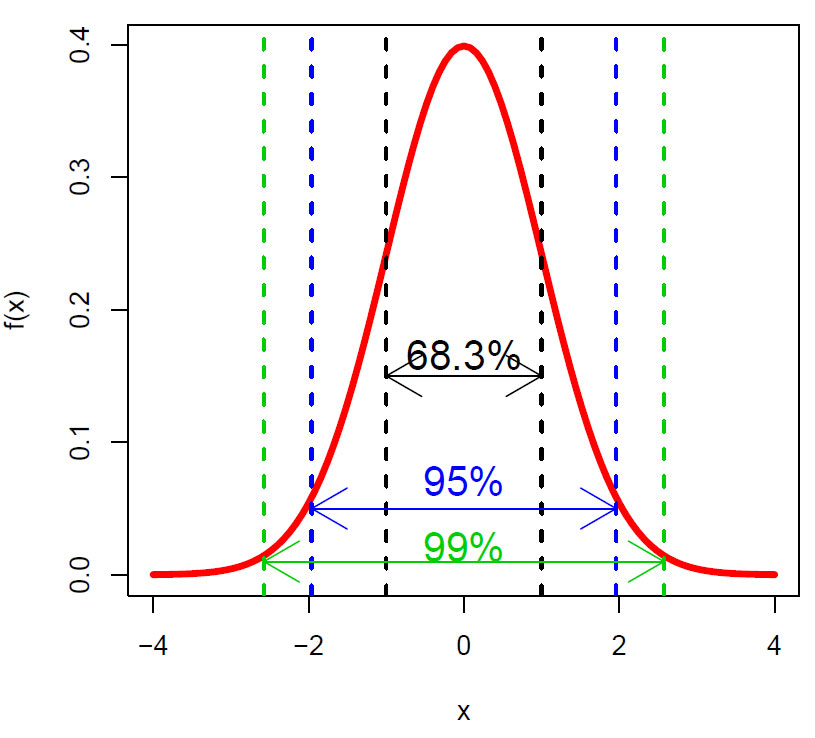
Arealet av normalfordelingskurven som ligger mellom pluss (+) minus (-) ett standardavvik tilsvarer ca. 68.3 % av arealet under kurven. Pluss minus 1.96 standardavvik tilsvarer 95% av arealet av kurven, de resterende 5% er fordelt med 2.5% i hver hale av kurven, relatert til p=0.05. Pluss minus 2.576 standardavvik tilsvarer 99% av areaeet under normalfordelingskurven.

Et histogram av frekvensene for 100000 pseudorandome slumptall fra standard normalfordeling, og den kontinuerlige kurven sannsynlighetstetthetsfunksjonen.
Histogram og frekvensfordeling
Frekvensfordeling får man ved å telle og gruppere antall objekter/subjekter med en bestemt verdi eller verdiintervall. Høyden på kolonnene viser andel og antall av dataene som befinner seg innen hvert intervall. Sannsynlighetsfordeling er andelen er proporsjonen av antall objekter med en bestemt verdi, og kan uttrykkes i et histogram. En symmetrisk fordeling (eks. normalfordeling, students t-fordeling) kan brettes omkring en midtlinje, og de to halvdelene er speilbilder av hverandre. Mode er den vanligste respons, den det er flest av, og en fordeling med bare en topp kalles unimodal. Har den to topper er den bimodal. En venstreskjev fordeling har lang hale til venstre. En høyreskjev fordeling har lang hale til høyre.

Omregning til z-skår og standard normalfordeling. Histogrammet til høyre (oransje) bekskriver histogrammet for 10000 slumptall fra normalfordelingen med gjennomsnitt lik 4 og standardavvik 0.5. Tallene er deretter omregnet til standard normalfordeling med gjennomsnitt lik 0 og standardavvik lik 1 (lysegrønn).
\(z=\displaystyle\frac{x-\mu}{\sigma}\)

Normalfordelingen med gjennomsnitt=0, med forskjellige standardavvik. Kurven for standard normalfordeling har standardavvik = 1 (rød), det vil si µ = 0 og standardavvik for populasjonen σ = 1.
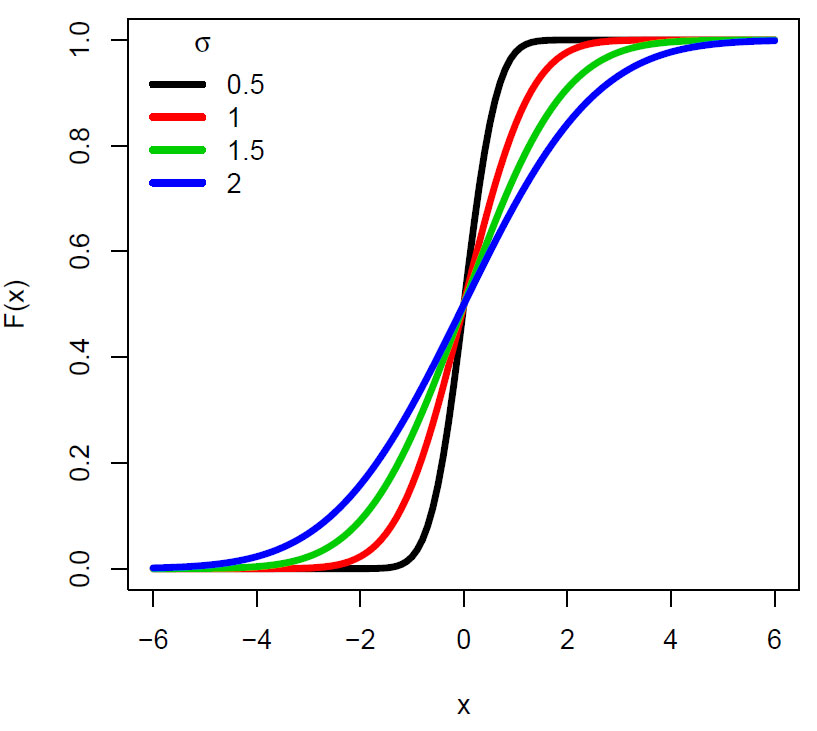
Den kumulative sannsynlighetsfunksjonen F(x) for en normalfordeling med gjennomsnitt lik 0 og forskjellige standardavvik. Legg merke til y-aksen går fra 0-1, det vil si det samme som sannsynlighetene p=0-1. Den rød kurven er for standard normalfordeling.
Normalfordelingen ble først oppdaget av den franske matematikeren Abraham de Moivre som også kunne vise at den diskrete binomiale sannsynlighetsfordelingen konvergerer mot normalfordelingen, et resultat av sentralgrenseteoremet. de Moivre oppdaget også Stirlings formel. Normalfordelingen har en rekke nyttige egenskaper. Hvis man har to uavhengige normalfordelte tilfeldige variable X og Y så er summen av dem også en normalfordelt variabel med forventet verdi E(X+Y)=E(X)+E(Y) og Var(X+Y)=Var(X)+Var(Y).
Både Poisson-, binomial-, negativ binomial- og gamma-fordelingen for diskrete variable, og gjennomsnittene fra dsse kan under gitte betingelser følge normalfordeling, også et resultat av sentralgrenseteoremet. Løsningen av differensialligningen for Ficks andre diffusjonslov har store likhetstrekk med sannsynlighetstetthetsfunksjonen for nomalfordelingen.
Kvantilfunksjonen
Kvantilfunksjonen er den inverse funksjonen av den kumulative sannsynlighetsfunksjonen
F(x), hvor x- og y-aksen bytter plass, noe som gjør dem mer anvendelige. Den kumulative sannsynlighetsfordelingen F(x) lik p= g(x) og kvantilfunksjonen er inverse funksjoner,
\(p= g(x)\;\;\;\;\;\;\; \text{og}\;\;\;\;\;\; x= g(p)^{-1}\)
p-kvantilene til sannsynlighetsfordelingen g(x) en stokastisk variabel x i området [-∞,∞].
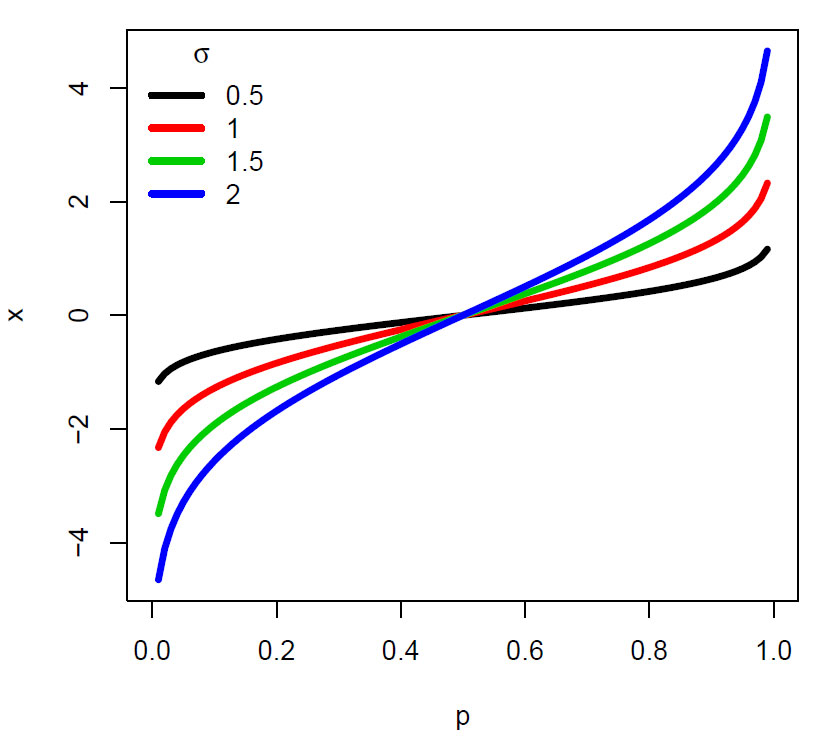
Kvantilfunksjonen for normalfordelingen med gjennomsnitt lik 0. Den røde linjen angir kvantilfunksjonen for en standard normalfordeling.
Forventning E(X) fra en kontinuerlig sannsynlighetsfordeling
For en kontinuerlig sannsynlighetsfordeling har vi at forventningen E(X) er lik:
\(E(X)= \displaystyle\int_ {-\infty}^\infty x\:f(x)dx\)
Vi lager en grafisk framstilling av hvor f(x) er sannsynlighetstetthetsfunksjonen for en standard normalfordeling:
\(y= x \cdot f(x)\)
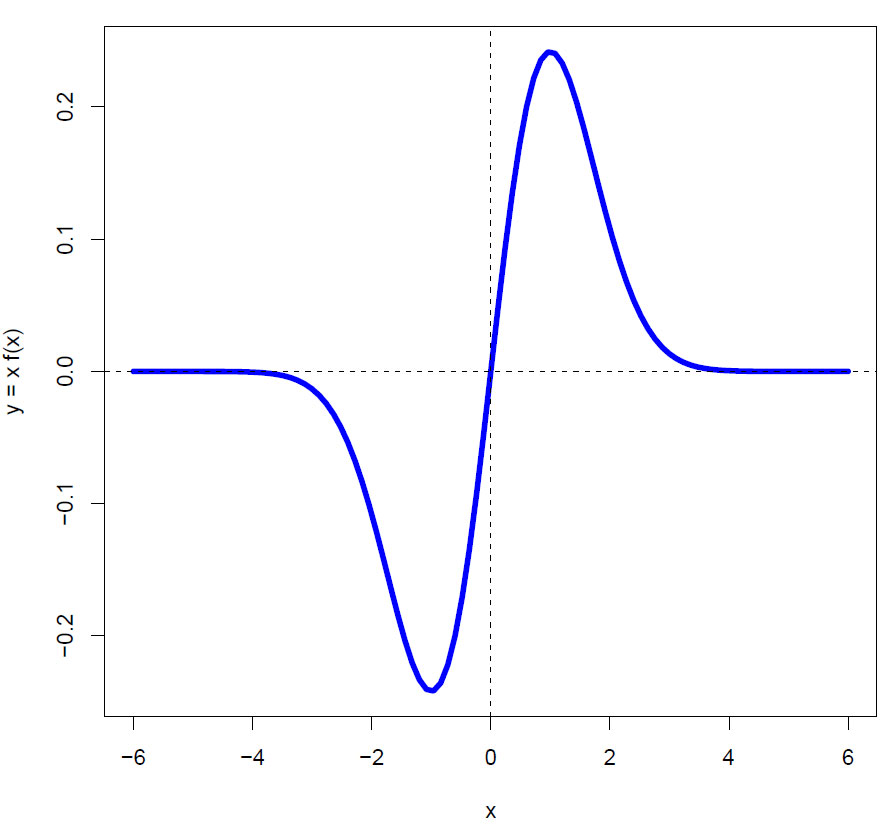
Figuren viser integranden y= xf(x) hvor f(x) er sannsynlighetstethetsfunksjonen for en standard normalfordleing:Gjennomsnittet eller forventningen E(X) for en standard normalfordeling er lik 0, og vi kan se av figuren at integrerer man hele figuren blir arealet lik 0 (like store arealer over og under x-aksen.
Normalfordeling og Z-skår
En normalfordelingskurve er bestemt av standardavvik mu (μ) og varians sigma (σ2), skrevet som X~N(μ,σ2). I en standard normalfordeling settes gjennomsnittsverdien μ=0 og variansen beregnes som antall standardavvik lik 1, altså Z~N(0,1). Univariat normalfordeling benyttes på alle typer målbare data, vekt, lengde. Den kan lett standardiseres til en standard skala. X blir transformert til Z hvor Z følger normalfordeling med gjennomsnitt lik 0 og standardavvik lik 1:
\(Z=\displaystyle\frac{X-\mu}{\sigma}\)
Z-skår (Z) er et mål på antall standardavik som en dataverdi er vekk fra gjennomsnittsverdien µ. Z-skår er praktisk å bruke når man skal sammenligne verdier fra forskjellige datasett.
Hvis X er 1 standardavvik vekk fra gjennomsnittsverdien (middelverdi, forventet verdi) så blir Z=1
\(X= \mu + \sigma\;\;\;\;\;\; \implies\;\;\; Z= \displaystyle\frac{\mu + \sigma-\mu}{\sigma}= 1\)
Hvis X er 2 standardavvik vekk fra gjennomsnittsverdien så blir Z=2
\(X= \mu +2 \sigma\;\;\;\;\;\; \implies\;\;\; Z= \displaystyle\frac{\mu + 2\sigma-\mu}{\sigma}= 2\)
Når X > (større enn) gjennomsnittsverdien blir Z>0, og når X < (mindre enn) gjennomsnittsverdien blir Z<0
I standard normalfordeling sannsynlighetstabell som vi finner bak i noen statistikkbøker, så angir disse arealet under standard normalfordelingskurve (tetthetskurven) fra -∞ til z, kumulativ sannsynlighetsfordeling F(z):
\(F(z)= \displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\infty}^ze^{-\frac{1}{2}\left(\frac{X- \mu}{\sigma}\right)^2 }dx= P(Z\leq z)\)
Det er denne fordelingen man finner i statistiske tabeller og viser arealet under standardnormalfordelingsfunksjonen i intervallet [-∞,z], altså til venstre for z.
Hvis vi integrerer fra minus uendelig til z= 1 tilsvarer det 84.13447 % av arealet under kurven for standard normalfordeling.

Vi kan finne kritiske tabellverdier for Z=-1.96, -1, 0 ,1, 1.96, som blir henholdsvis 0.9750, 0.8413, 0.5000, 0.1587, og 0.0250.

I et normal kvantilplot rangeres datapunktene og persentilrang omdannes til Z-skår. Z-skår plottes på x-aksen og datapunktene på y-aksene. Dette gir en rett linje hvis normalfordeling.
Kvantilene er lik summen av arealet under standard normalfordeling fra [-∞,zα] for forskjellige sannsynligheter α (p). De samme som du finner bak i statistikkbøker som tabell over kumulativ standard normalfordeling.
Hvis vi har en tilfeldig variabel X som er normalfordelt med gjennomsnitt µ=2 og standardavvik σ=0.5, så blir z=(X-2)/0.5 fordelt etter standard normalfordeling med gjennomsnitt=0 og standardavvik=1.
Hva er sannsynligheten for at en slik variabel befinner seg i intervallet Pr{1.6≤X≤2.4} ? Vi regner om til z-skår (-0,8 og 0.8) og finner det tilsvarende areal under standard normalfordeling i dette intervallet, i eksemplet tilsvarer det 57.6% sannsynlig.
Statistisk inferens
Vi forsøker å ta ut en mest mulig representativ prøve fra populasjonen. Prøven er en undermengde av populasjonen.
Utkomme for en prøve følger en statistisk fordeling. Et representativt uttrykk for forventningen er gjennomsnittet eller den sentrale tendens. Ved gjentatte målinger fra samme populasjon kan man beregne gjennomsnittet, summen av alle enkeltmålingene dividert på antall målinger.
\(\overline x= \displaystyle\frac{\sum_{i= 1}^n x_i}{n}\)
Middelverdien (gjennomsnittsverdien) er et vektet gjennomsnitt av alle verdiene av X fordi alle utkomme er ikke nødvendigvis like. Gjennomsnittsverdien er praktisk siden man med å angi tallet for den med måleenhet har angitt hvor den sentrale tendens befinner seg, og med et spredningsmål (varians) eller standardavvik viser man hvoran måleresultatene sprer seg rundt gjennomsnittsveriden. Middelverdien (gjennomsnittsverdien) av en tilfeldig variabel X kalles forventet (ekspektert) verdi av X. Middelverdien for en kontinuerlig tilfeldig variabel er senter av en mer eller mindre symmetrisk tetthetskurve. Når antall observasjoner øker så vil middelverdien nære seg den sanne verdien for gjennomsnittet, µ. Vi bruker de greske bokstavene mu ( µ) og sigma (σ) for henholdsvis middelverdi og varians for de sanne verdiene som vi aldri finner, men som vi lager et estimat av i vårt forsøk ved å lage et konfidensintervall. For α=0.05 (eller p=0.05) så tilsvarer
\(\mu \pm 1.96 \cdot \sigma\)
ca. 95% av arealet under normalfordelingskurven.
\(\mu \pm \sigma\)
tilsvarer ca. 68.3 % av arealet under normalfordelingskurven.
Standardavviket for prøven (s) er kvadratroten av kvadrerte avvik fra gjennomsnittet dividert på n-1. Legg merke til at vi bruker s når det er snakk om standardavviket til prøven og den greske sigma σ for standardavviket til populasjonen.
\(s= \displaystyle\sqrt{\frac{\sum_{i= 1}^n (\overline x-x_i) ^2}{n-1}}\)
Vi dividerer på antall frihetsgrader n-1, siden vi har brukt opp en frihetsgrad i utrening av gjennomsnittsverdien.
Hvis man gjør gjentatte uttak av prøver fra populasjonen og beregner gjennomsnittet for hver gang, så vil gjennomsnittene følge normalfordeling (sentralgrenseteoremet).
Standardfeilen (SE), standardavviket til gjennomsnittene, er lik:
\(SE=\displaystyle\frac{\sigma}{\sqrt{n}}\)
Ingenting i statistikk er absolutt, og i enhver statistisk analyse er det en tilfeldighetsfaktor. Hypotesetesting gir grunnlag for statistisk inferens. Vi trenger et kriterium for å kunne avgjøre om vi aksepterer hypotesen eller ikke, og til dette bruker vi alfa (α), og jo lavere verdi for α desto mer stringent er testen. Vanligvis settes α=0.05, som tilsvarer 5% av arealet under sannsynlighetstetthetskurven, for en tohalet test 2.5% i hver ende.
Når man gjør en hypotesetest er det fire mulige utkomme, hvorav to representerer en ”riktig” avgjørelse. Man forkaster en ”usann” hypotese , og aksepterer en ”sann” hypotese. Type I-feil er forkasting av nullhypotesen H0 gitt at H0 er sann.
Type II-feil er hvor man ikke forkaster en flask nullhypotese, og bestemmes av beta (β). Teststyrken er 1-β. Når prøvestørrelsen øker så øker teststyrken. Ved å senke verdien av α så minsker teststyrken, en test med α=0.01 har lavere teststyrke sammenlignet med en hvor α=0.05. Ikke bland sammen begrepene teststyrke og signifikansnivå.
Vi kan for eksempel til å finne teststyrken for t-tester.hvis n=30, α=0.05 og en en-prøve t-test, hvor vi ønsker å finne en forskjell på 0.6 enheter mellom nullhypotesen og alternativ hypotes så vil utfallet om teststyrke i statistikkprogrammet du vise at i ca. 89% av tilfellene vil nullhypotesen bli forkastet som den skal i dette tilfellet.
Numerisk funksjonsanalyse av normalfordelingskurven
Funksjonen f(x) beskriver fordelingen av en kontinuerlig normalfordelt variabel
X ~ N(µ, σ2)
\(f(x)= \displaystyle\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{X- \mu}{\sigma}\right)^2 }\)
parameter µ (mu) er gjennomsnittsverdien eller forventningen til fordelingen (E(X), som i dette tilfelle også blir lik median og mode. Parameter σ2 (sigma) er varians (Var(X)) og σ, kvadratroten til variansen er lik standardavviket. I en standard normalfordeling er µ = 0 og σ = 1.
Vi lager først en figur for sannsynlighetstetthetsfunksjonen for en standard normalfordleing. Vi lager et plot av den førstederiverte på den samme figuren. Finner den andrederiverte ved å derivere den førstederiverte. Lager en plot av den andrederiverte på den samme figuren og har forskjellige farger for å skille sannsynlighetstetthetsfunksjonen f(x) (blå) den førstederiverte f’(x) (rød) og den andrederiverte f’’(x) (grønn). Hva forteller den første- og andrederiverte om maksimum- og minimumspunktene, samt vendepunktene på normalfordelingskurven ? For maksimumspunktet er den førstederiverte lik 0. Ved x=-1 og x = 1 er det vendepunkter på normalfordelingskurven. Den andrederiverte angir om normalfordelingskurven stiger eller avtar. Finner røttene til den førstederiverte. Finne røttene betyr å finne verdien for x når f’ (x) = 0. Hvilken y-verdi har du på toppen av kurven for standard normalfordeling ? Jo,
\(\frac{1}{\sqrt{2\pi}}= 0.3989423 \dots\)
Nå skal vi finne vendepunktene til normalfordelingsfunksjonen i x-intervallet [-2, 2], samt vendetangentene ved å benytte den andrederiverte. Først finner du røttene til den andrederiverte. Se at vendepunktene blir ved -1 og 1. Finner den tilsvarende y-verdien i vendepunktene. Stigningstallet til vendetangenten er gitt via den førstederiverte.
Funksjonen for en rett linje er:
\(y= \beta _ 0 + \beta_1 x\)
hvor β0 er skjæringspunkt (intercept) og β1 er stigningstall (slope) . Siden vi nå allerede har funnet stigningstallet (slope) og kjenner verdien for x i vendepunktet så kan vi finne skjæringspunktet med y-aksen. Lager et plot av vendetangentene på den samme figuren.

Funksjonsanalyse av sannsynlighetstetthetsfunksjonen for en standard normalfordeling f(x) (blå). Ved numerisk derivasjon bestemmes funksjonen for den førstederiverte f'(x) (rød). Legg merke til at den førstederiverte er lik 0 ved maksimumspunktet. Når du går fra venstre mot høyre for den førstederiverte ser du at først stiger f(x) til du kommer til vendepunktet x=-1, så synker den deriverte, dvs. f(x) flater av inntil den når maksimumspunktet (rød prikk). Den førstederiverte er deretter negativ, det betyr at f(x) synker, og det gjør den inntil vendepunktet x=1, Vi ser at den andrederiverte f''(x) (grønn) er negativ ved maksimumspunktet.
Numerisk integrasjon med Riemannapproksimasjon
Man kan beregne arealet under en kurve ved å summere en rekke rektangler som følger kurven under et gitt intervall [a,b], jo flere rektangler, desto mer nøyaktig integral. Hvis vi har et areal under en ikke-negativ kontinuerlig funksjon y=f(x) avgrenset av intervallet [a,b] hvor a ≤ x ≤b, så kan intervallet [a,b] deles inn i n delintervaller med lik lengde:
\(\Delta x= \displaystyle\frac{b-a}{n}\)
I statistikk er det behov for å kunne beregne sannsynligheten for at en kontinuerlig tilfeldig (stokastisk) variabel X befinner seg i et intervall [a, b].
Riemannintegraelet er summen av arealet av en mengde rektangler under kurven hvor høyden bestemmes av f(x). Arealet av det første rektangel blir Δx∙f(x1) osv. Vi kan lage en Riemann sum for funksjonen f kalt Sn(f) og arealet blir grenseverdien for denne summen når n → ∞
\(S_n(f)= f(x_1)\Delta x + f(x_2) \Delta x + f(x_3) \Delta x + \dots + f(x_n)\Delta x\)
Når antall rektangler øker så minsker bredden av dem og vil etter hvert gå mot 0. Det summerte arealet tilsvarer ca. integralet (Riemannapproksimasjon).
\(\displaystyle\int_ a^b f(x)dx= \lim\limits_{n \to \infty} \sum_{i= 1}^n f(x_i) \Delta x\)
Hvis f(x) er negativ for noen verdier lages rektangler under x-aksen, og man trekker arealene over og under x-aksen fra hverandre slik at man ender opp i et endelig areal.
Gjennomsnittsverdien for f(x) i intervallet [a,b] blir:
\(\text{Gjennomsnittsverdi for f}= \displaystyle\frac{1}{b-a}\int_a^b f(x)dx\)
Vi skal først estimere arealet under sannsynlighetstetthetsfunksjonen for standard normalfordeling -+ ett standardavvik.
Standard normalfordeling er gitt ved formelen:
\(f(x)= \displaystyle\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\)
Sannsynligheten for at X ligger i intervallet [a,b]:
\(P(a<X\leq b= \displaystyle\int_a ^b f(x)dx\)
Først setter vi øvre og nedre grense for a og b, her -1 til 1. Deretter lager vi 10 rektangler, og deler inn intervallet [a,b] i 10 deler. Vi lager en midtlinje i hver av rektanglene. Så lager vi punkter som ligger på kurven f(x) for hver av midtlinjene. Til slutt plotter vi rektanglene. Riemannintegralet blir lik summen av arealet av de 10 rektanglene. Nå ønsker vi å finne et mer nøyaktig integral ved ¨å øke antall rektangler for eksempel til n = 10000, og setter nedre grense a = -1 og øvre grense b = 1.
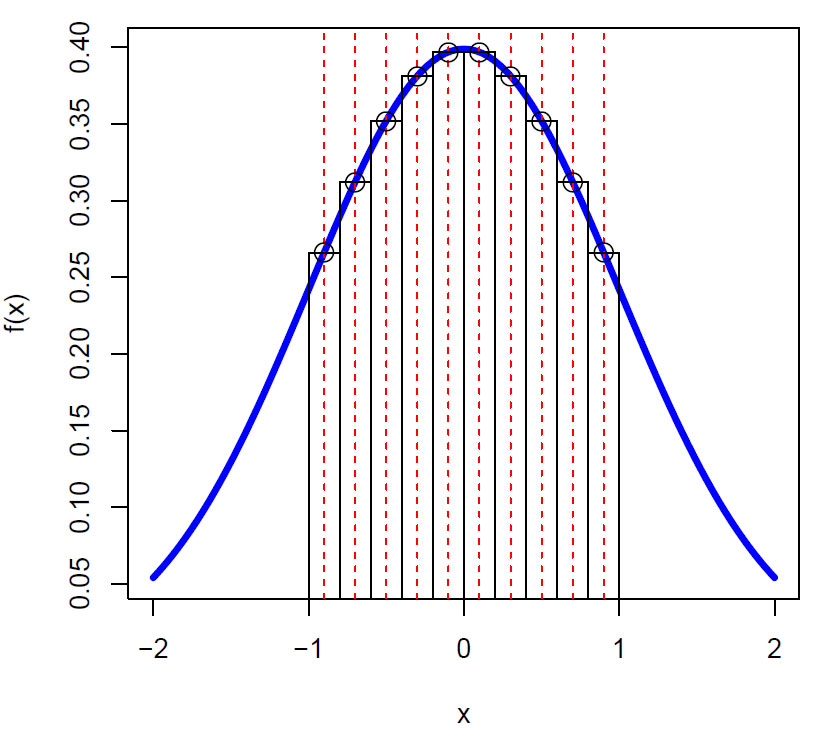
Riemannapproksimasjon av arealet under en standard normalfordeling i intervallet -1 til +1 standardavvik fra gjennomsnittet lik 0
Resultatet blir 68.26% av totalarealet.
Integrasjon med Monte-Carlo-metode.
Vi skal foreta integrasjon av kurven for standard normalfordeling ved bruk av Mont-Carlo.
Lager et rektangel rundt normalfordelingskurven i intervallet med x-verdier fra [-1, 1] and y-verdier [0, 0.4]. Nå skal vi putte et stort antall tilfeldige punkter inn i rektangelet og finne ut hvor mange av dem som befinner seg under sannsynlighetstetthetskurven. Dette blir et mål på arealet. Som tidligere lag et plot av standard normalfordeling, men nå begrenset av x-verdiene i intervallet [-1, 1]. Deretter trekker vi ut hundre tusen tilfeldige punkter fra den uniforme sannsynlighetsfordelingen i det angitt intervallet. Siden tallene egentlig er pseudotilfeldige finnes det metoder for å få slumptallsgeneratoren til å starte på samme sted hver gang. Vi velger nå ut punkter som er mindre enn normalfordelingskurven, og finner gjennomsnittet av dem, i dette tilfellet areal: 0.682904. Det blir litt forskjellig for hver gang, men er et estimat.
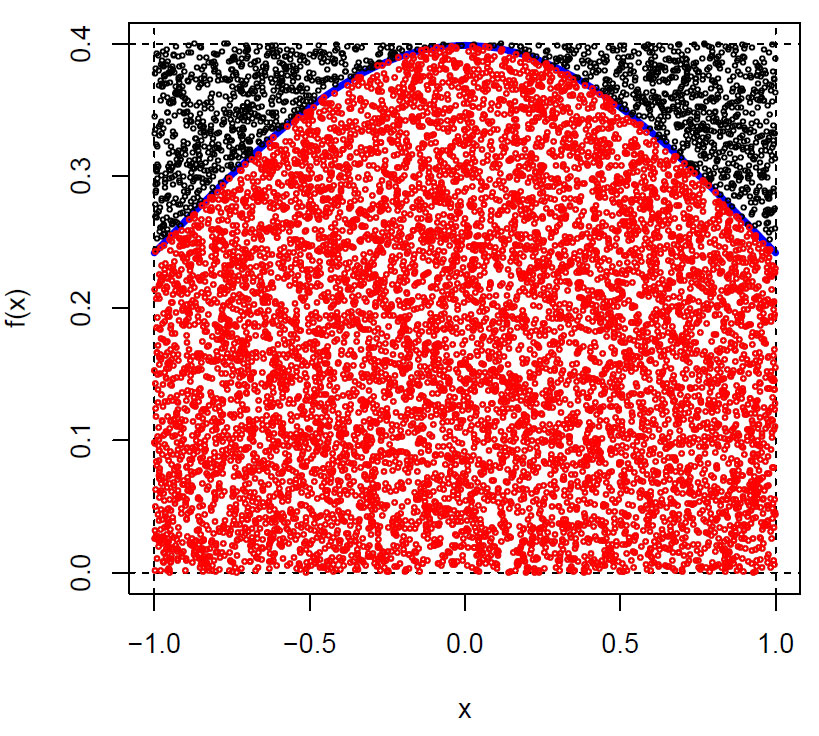
På figuren vises er det bare vist noen av de hundretusen punktene.
Litteratur
Mer om derivasjon og integrasjon.
Alle figurene vist på denne siden er laget i det objektorienterte programmerings- og statistikkspråket R, og her er en bruksanvisning for hvordan det kan gjøres. Og det fine: metodene som er vist kan du anvende på en hvilken som helst funksjon som du ønsker å studere nærmere. Det kan være fint å lære programmeringsspråket Python, men alt du kan gjøre i Python kan du gjøre i R.
R Core Team (2019). R: A language and environment for statistical
computing. R Foundation for Statistical Computing, Vienna, Austria.
URL https://www.R-project.org/.
Wikipedia