Det irrasjonale og transendentale tallet pi (π)= 3.1415926535897932384626433...
At pi er et irrasjonalt tall vil si at det ikke kan uttrykkes som et eksakt tall fra en brøk med to heltall, og desimalene fortsetter i det uendelige. Pi-desimalene virker tilfeldige, tallene 0-9 forekommer tilsynelatende tilfeldig uniformt ifølge statistiske tester, men er allikevel ikke så tilfeldige som man tror.
Pi er også transcendentalt, det vil si at det kan ikke være roten i et algebraisk polynom med rasjonale koeffisienter. Det betyr at å konstruere med bare passer og lineal et kvadrat med like stort areal som en sirkel blir umulig (sirklens kvadratur). Pi kan uttrykkes som et uendelig antall brøker i delbrøkoppspalting.
Hvorfor treffer vi på tallene pi (π), det naturlige tallet e og gamma (γ) så mange steder og sammenhenger ?
Tallkonstantene π, e og γ har mennesket klart å fravriste naturen i lang tids søken etter hvordan vår verden er skrudd sammen av småbiter og bestanddeler, og styrt av fysiske, kjemiske og biologiske lover.
Tallet pi er forholdet mellom omkretsen (O) av en sirkel og diameteren (d=2r, hvor r er radius) til sirkelen. Uansett hvilken sirkel man har så gjelder denne sammenhengen:
\(\displaystyle \pi=\frac{\text{omkrets}}{\text{diameter}}= \frac{O}{d}\)
Omkretsen (O)av en sirkel med radius r:
\(\displaystyle O=2\pi r\)
Arealet (A) til en sirkel med radius r:
\(\displaystyle A=\pi r^2\)
Volumet (V)av en kule med radius r:
\(\displaystyle V=\frac{4}{3}\pi r^3\)
Overflate (OF) av en kule med radius r:
\(OF=4\pi r^2\)
Hva er volumet av en pizza med radius z og høyde a ? jo: pizza.
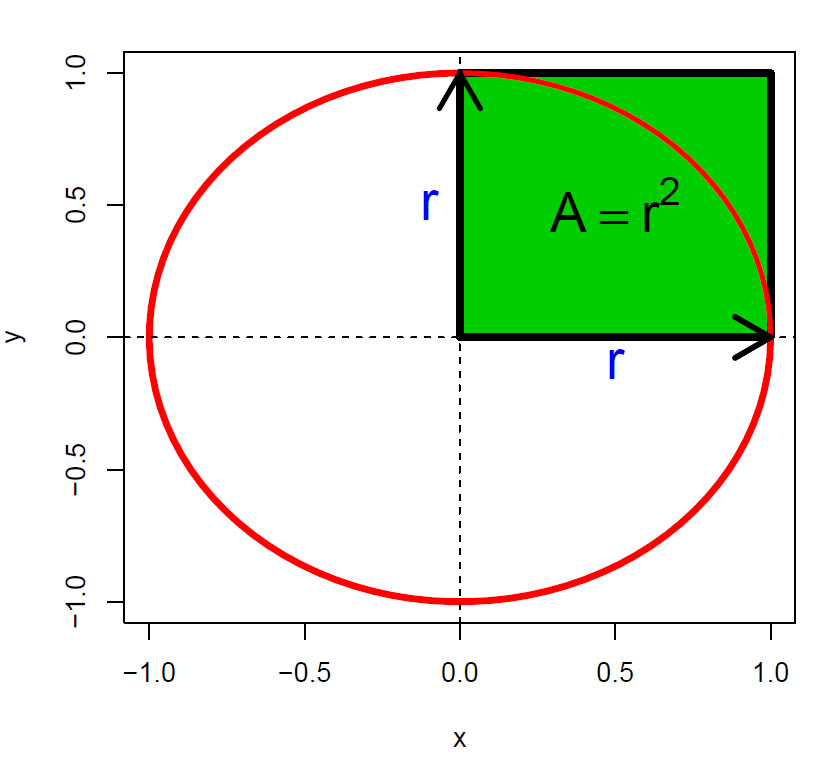
Arealet til en sirkel er π ganger arealet av den grønne firkanten på figuren (πr2). Omkretsen av en sirkel er 2π radianer. cos(x) og sin(x) vil bli liggende på enhetssirkelen fordi:
\(\displaystyle \cos ^2 x + \sin ^2 x=1\)
Formelen for en enhetssirkel er:
\(\displaystyle x^2 + y^2 = 1\)
Derav følger:
\(\displaystyle y= \sqrt{1-x^2}\)
Integralet som gir halve enhetssirkelen blir:
\(\displaystyle\int_{-1}^1 \sqrt{1-x^2}dx=\frac{\pi}{2}\)
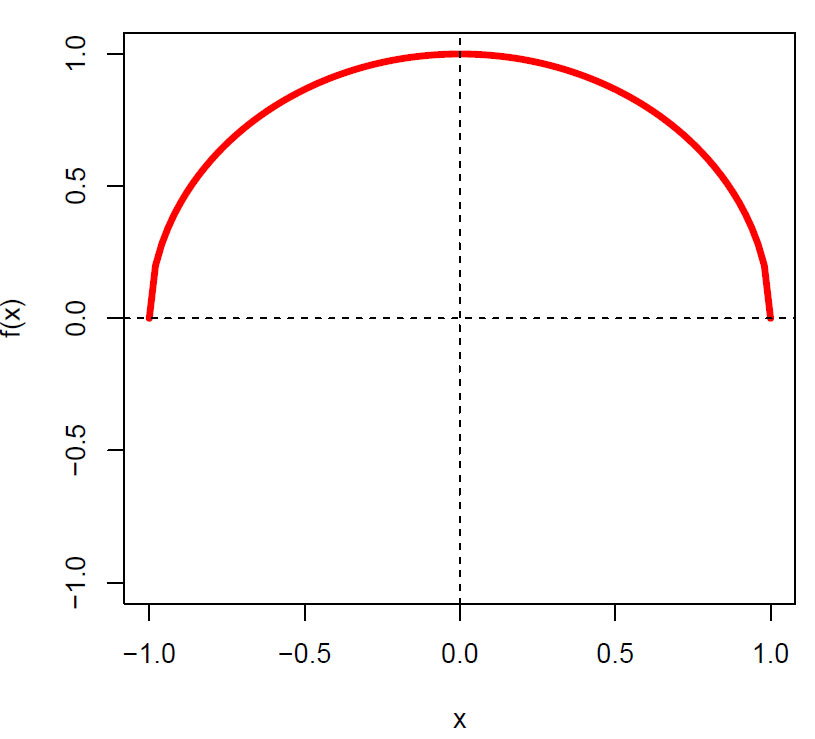
Arealet under en halv enhetssirkel er pi halve.
Man finner igjen π også i geometriske figurer som baserer seg på sirkelen som ellipse og kjegle (kjeglesnitt).
For en n-dimensjonal kule med radius r blir overflatevolumet Vn:
\(\displaystyle V_n= \frac{\pi ^{\frac{n}{2}}}{\Gamma\left(\frac{n}{2}+1\right)}r^n\)
hvor Γ er gammafunksjonen.
Vi ser at for n=3 så blir svaret lik volumformelen over:
\(\displaystyle V_3= \frac{\pi ^{\frac{3}{2}}}{\Gamma\left(\frac{3}{2}+1\right)}r^3=\frac{\pi ^{\frac{3}{2}}}{\Gamma\left(\frac{5}{2}\right)}r^3 \)
Overflaten av en n-dimensjonal kule OFn blir:
\(\displaystyle OF_n=\frac{n\pi^{\frac{n}{2}}}{\Gamma\left(\frac{n}{2}+1\right)}r^{n-1}\)
Gammafunksjonen er også relatert til π:
\(\displaystyle \Gamma\left(\frac{1}{2}\right)= \sqrt{\pi}\;\;\;\;\;\; \Gamma\left(\frac{5}{2}\right)= \frac{3}{4}\sqrt{\pi}\)
Arkimedes kunne finne et estimat av pi ved henholdsvis å omskrive og innskrive sirkelen med regulære polygoner og beregne perimeterverdien av sidekantene. For et regulært polygon med 96 sider fant han at pi måtte befinne seg i intervallet 223/71< π <22/7.
Det kom ny utvikling i estimering av pi med konvergerende uendelige tallrekker (tallfølger) introdusert av Gottfried Wilhelm Leibniz, Hohn Wallis, Isaac Newton, James Gregory, John Machin inspirert av indiske astronomer og matematikere. En utgave av
Gregory-Leibniz-rekken med invers tangens konvergerer mot π/4 for x=1
\(\displaystyle arctan \;x = x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+ \frac{x^9}{9}-\dots\)
\(\displaystyle \frac{\pi}{4}= arctan\; (1)= \displaystyle\sum_ {n=0}^\infty \frac{(-1)^n}{2n+1}\)
En annen utgave av Gregory-Leibniz-rekken konvergerer mot pi:
\(\displaystyle \pi= \frac{4}{1}-\frac{4}{3}+ \frac{4}{5}-\frac{4}{7}+ \frac{4}{9}- \frac{4}{11}+ \frac{4}{13} \dots\)
Ifølge Eulers formel er det uendelig mange primtall, hvor p er et primtall:
\(\displaystyle\sum_{n= 1}^\infty \frac{1}{n}= \prod \frac{1}{1-\frac{1}{p}}\)
Eulers løsning av Basel-problemet i 1735 med opprinnelse fra Bernoulli er en utgave av Riemanns zetafunksjon for s=2
\(\displaystyle \zeta(s)= \displaystyle\sum_ {n= 1}^\infty \frac{1}{n^s}\)

Eulers form for Riemanns zetafunksjon, hvor p er et primtall:
\(\displaystyle\sum_{n= 1}^\infty \frac{1}{n^s}= \prod_{p \in P}\frac{1}{1-p^{-s}}\)
Euler kunne vise at den uendelige rekken eller tallfølgen ζ(2) konvergerer mot π2/6 og tallfølgen ζ(4) konverger mot π4/90.
Det er en kobling mellom primtallene ζ(1), pi og Riemanns zetafunksjon. Selv om den greske bokstaven π var tidligere blitt brukt for O/d så var det Eulers bruk av den i Introduction in analysin infinitorum som ga utbredelsen.
Den stadige søken etter flere desimaler i pi kom med iterasjoner av bl.a. arctangensalgoritmen eller Gauss-Legendre algoritmen på datamaskiner, for eksempel John von Neumann på ENIAC.
Srinivasa Ramanujan har funnet fram til flere formler for pi.
Integralet av Cauchyfordelingen, som har likhetstrekk med normalfordelingen, men har lenger haler:
\(\displaystyle\int_{-\infty}^\infty \frac{1}{x^2 + 1}dx\approx \pi\)
Kompleksplanet og pi (π)
Et komplekst tall kan uttrykkes som et reelt tall og et imaginært tall med vinkel θ (theta) rotasjon mot klokka
\(\displaystyle z= r(cos \theta + i\sin \theta)\)
I kompleksplanet med reell akse (Re(z)) og imaginær akse (Im(z)) med enhet i2=-1
Ifølge Eulers formel er det en sammenheng med det naturlige tallet e, grunntallet i naturlige logaritmer og enhetssirklen i kompleksplanet
\(\displaystyle e^{i\theta}= \cos \theta + i\sin \theta\)

Ved å sette vinkelen lik π (hele omkretsen av en sirkel er 2π), så får man Eulers identitet som viser en sammenheng mellom de matematiske konstantene e, pi og i
\(\displaystyle e^{i\pi}+1 = 0\)
Det er n komplekse røtter som tilfredsstiller den komplekse ligningen, hvor z er et komplekst tall:
\(\displaystyle z^n-1=0\)
Røttene er for k=[0,1,2,…,n-1]
\(\displaystyle e^{\frac{2\pi i k}{n}}\)
\(\displaystyle z^6 - 1 = 0\)
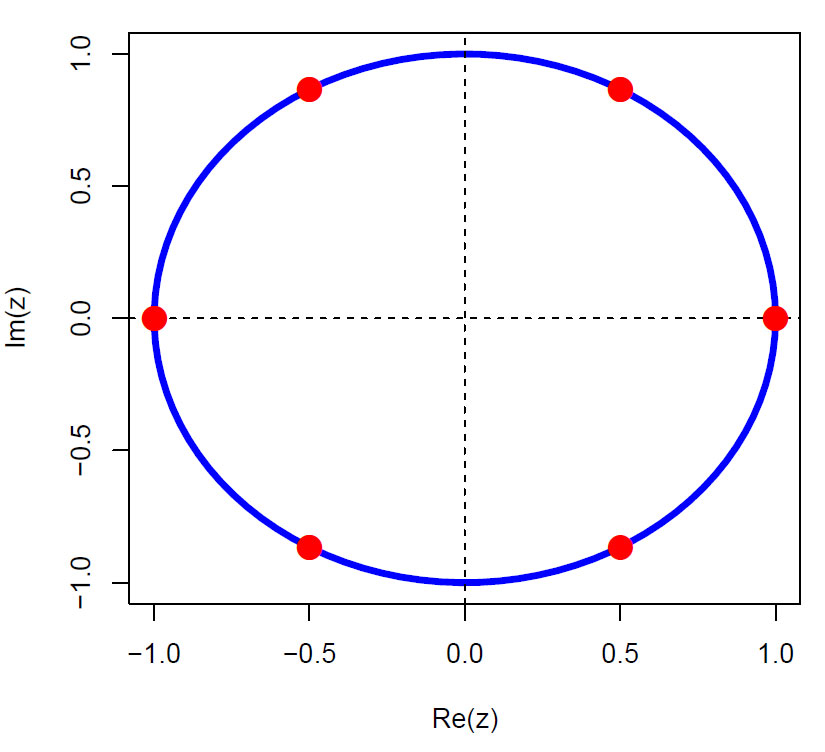
Figuren viser at røttene for z6-1=0 ligger på enhetssirkelen i kompleksplanet.
Stokes lov og π
Pi inngår også i en rekke fysiske konstanter som i Stokes lov i væskedynamikk hvor en kule beveger seg i en viskøs væske og blir utsatt for viskøse drakrefter F:
\(F=6\pi R\nu \eta\)
hvor R er radius, η (eta) er viskositet og v er hastighet.
Buffons nål og et estimat av π
Ved å slippe nåler ned på et ark med parallelle streker og telle hvor mange av nålene som var i kontakt med stripene kunne Buffon lage et estimat av π.
Mn kan også slippe blyanter ned på et parkettgulv eller tregulv med plankerer.
Pilkast og estimat av π
Ved å kaste dartpiler på en blink og registrere treffpunktene som (x,y-koordianter) i de fire kvadrantene kan man få et estimat av π. Pilkast og estimat av π.
Kultur
Historien om Pi (Life of Pi), film fra 2012 basert på History of Pi skrevet av den kanadiske foratteren Yann Martel.
Pi-dagen 14.mars (14.3) med internasjonal angivelse måned/ag er den 3.14.
Noen har grublet på hvordan vår verden villa ha sett ut hvis π hadde hatt en annen verdi, en underlig vridd hyperbolsk verden.
Litteratur
Apostol, T.M. Calculus (Vol I + II). Blaisdell Publ. Comp. 1962.
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.