e= 2.71828182845904523536028747135266249....
Tallet e er summen av en uendelig rekke hvor fakultetsfunksjonen n! inngår:
\(e= \displaystyle\sum_{n=0}^\infty \frac{1}{n!}\)
Eulers tall inngår som grenseverdi:
\(e=\lim\limits_{n \to \infty}\left(1 + \frac{1}{n}\right)^n\)
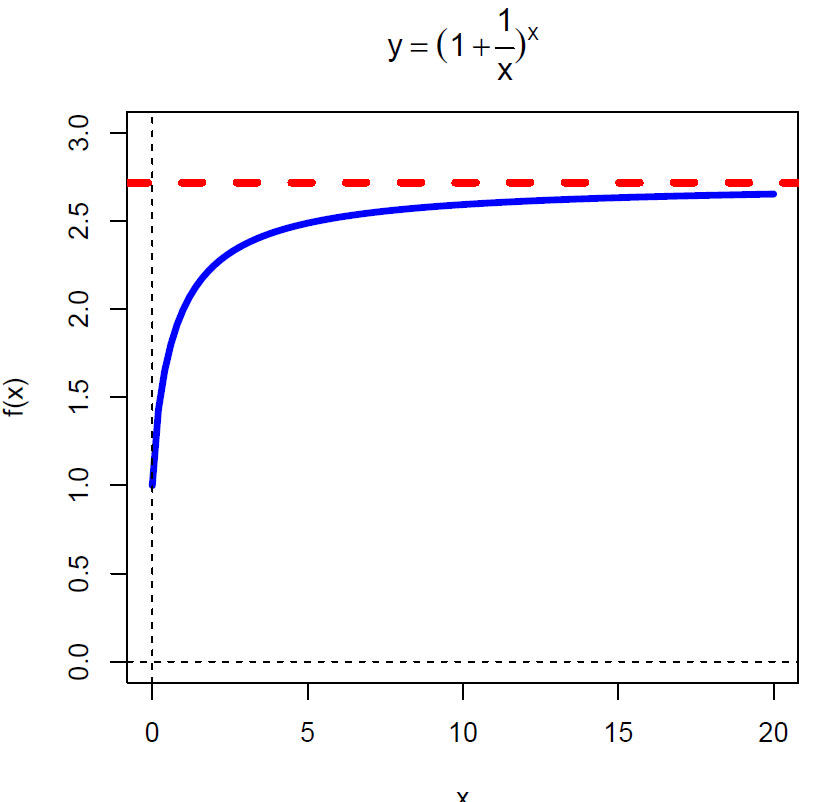
Funksjonen nærmerer seg asymptotisk til Eulers tall e.
Tallet e som grenseverdi:
\(e= \lim\limits_{x \rightarrow 0}\left(1+x\right)^{\frac{1}{x}}\)
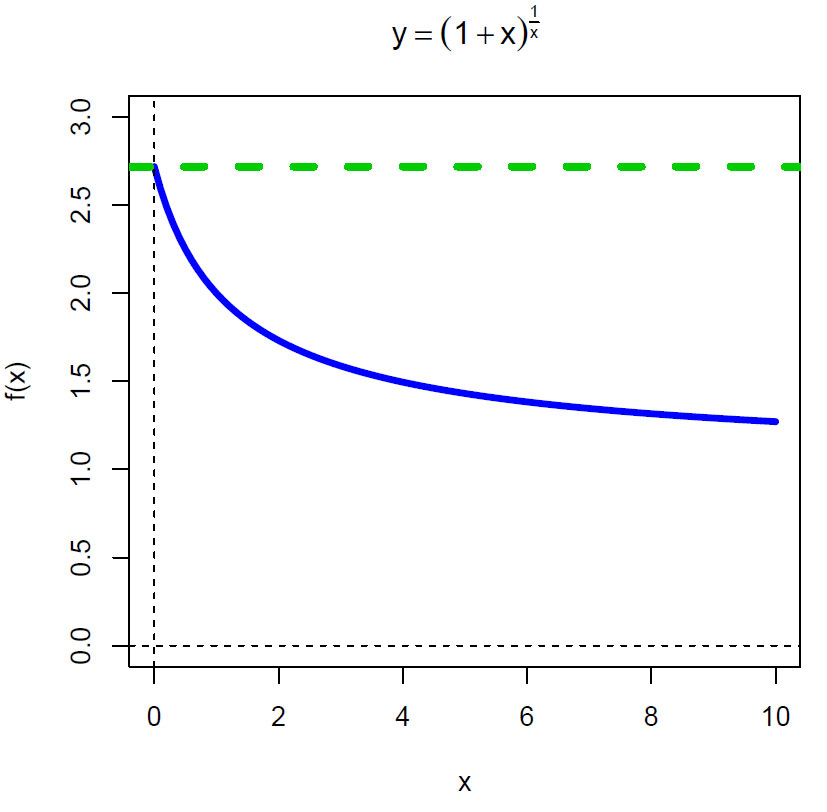
Kurven går mot tallet e når x → 0.

Eulers tall er også arealet mellom x-aksen og kurven y=1/x integrert mellom 1 og e.
\(\displaystyle\int_1^e \frac{1}{x}dx=1\)
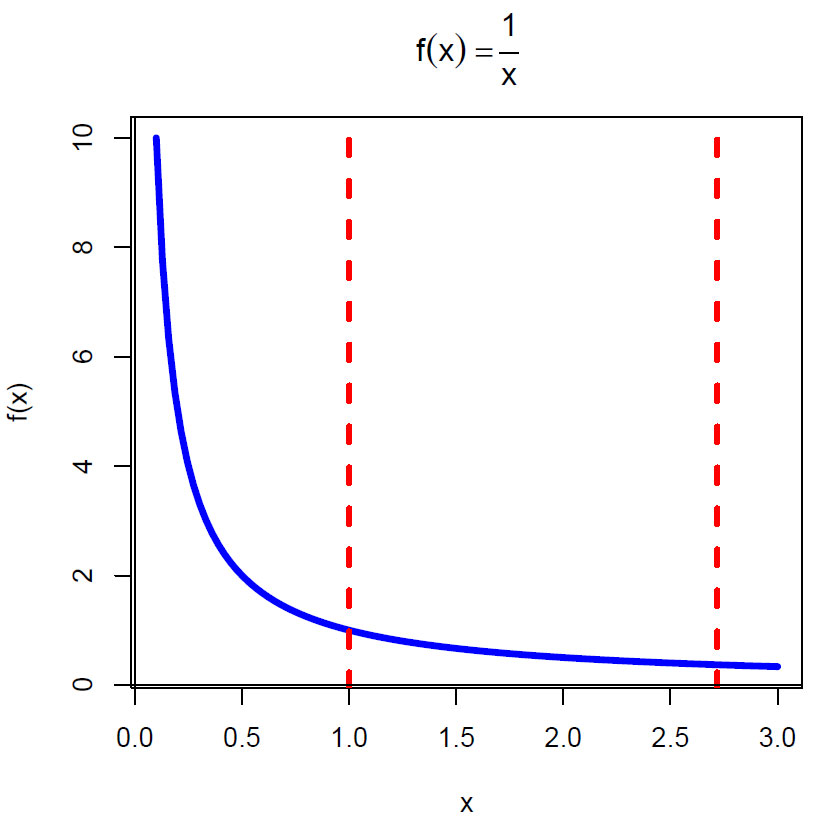
Intgralet av funksjonen y= 1/x fra 1 til e er lik 1.
Fakultetsfunksjonen n! stiger meget raskt med økende n, men Stirlings formel gir en asymptotisk tilnærming til fakultetsfunksjonen, og i denne inngår både e og π:
\(n!\approx \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n\)
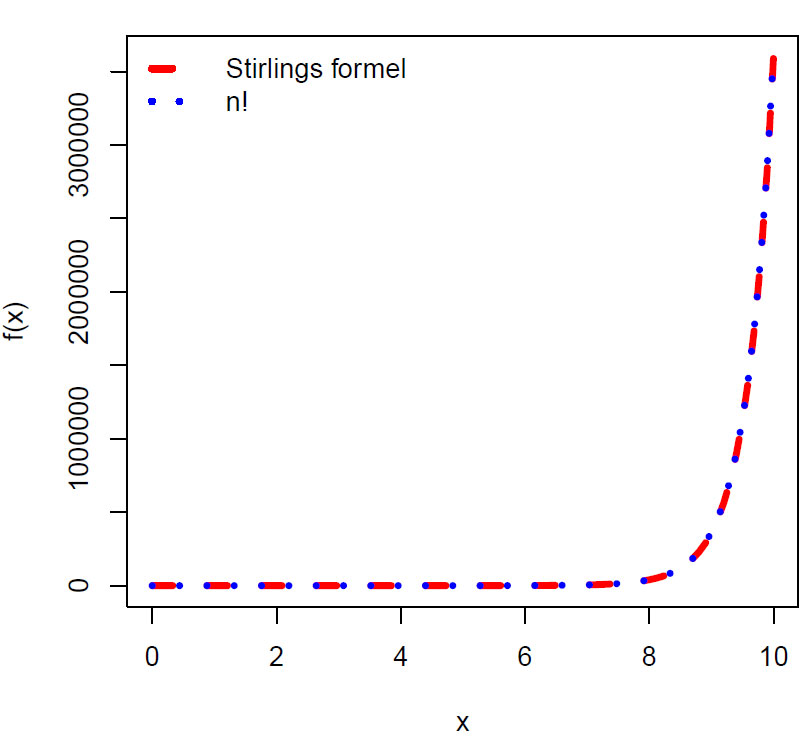
Fakultetsfunksjonen x! stiger meget rast med x, men Sterlings formel gir et godt estimat.
 '
'
Vi har også grenseverdien e når n går mot uendelig i funksjonen vist nedenfor:
\(e= \lim\limits_{n \to \infty}\frac{n}{^n\sqrt{n!}}\)

Den naturlige logaritmefunksjonen:
\(f(x)=\ln(x)\)
for e på x-aksen finner man at ln(e)=1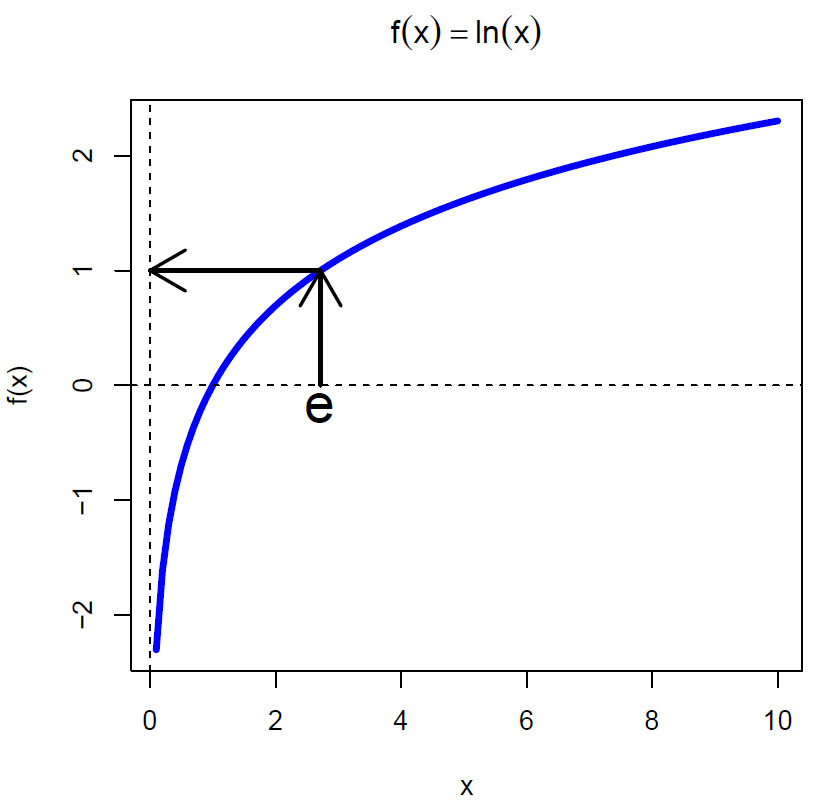
Logaritmefunksjonen med e som grunntall y= ln x, hvor ln(e)= 1. Logartimefunksjonen og eksponentialfunksjonen er inverse funksjoner.
Den deriverte av eksponentialfunksjonen er lik funksjonen selv:
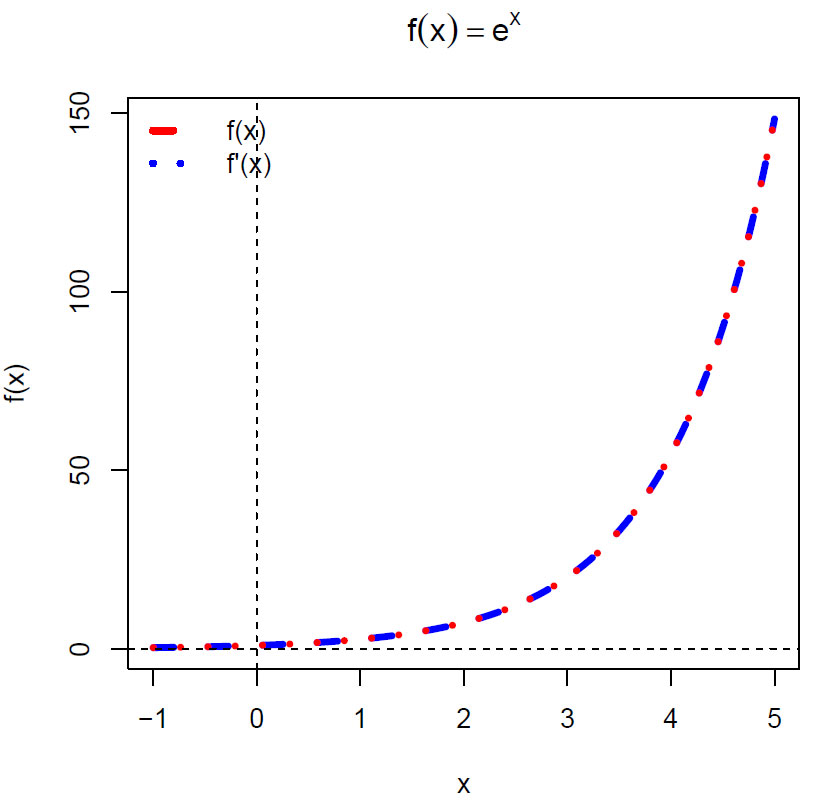
Eksponentialfunksjonen ex og dens deriverte er gir samme funksjon.
\(\frac{d}{dx}e^x= e^x\)
Derfor vil integralet av eksponentialfunksjonen være:
\(\int e^x dx=e^x + C\)
For differensialligningen:
\(\frac{dx}{dy}= y\)
så vil Cex være en løsning, hvor C er en integrasjonskonstant.
Vi finner e som maksimalpunktet for funksjonen:
\(f(x)= ^x\sqrt{x}\)

Eksponentialfunksjonen kan uttrykkes som et Taylor-rekke:
\(e^x =\displaystyle\sum_{n=0}^\infty \frac{x^n}{n!}= 1 + \frac{x}{1!}+ \frac{x^2}{2!}+ \frac{x^3}{3!}+ \dots \)
Ved å sette inn Taylor-rekke for sin(x) og cos(x) kan man utlede Eulers formel:
\(e^{i\pi}= \cos x + i\sin x\)
For x=e får vi:
\(e^{i\pi}= -1\)
For de komplekse tallene kan vi se at:
\(\ln(-1+0i)= i\pi\)