Parabel
Vi har en parabel:
\(y^2 = 4cx\)
Denne har brennpunkt F i (c,0), og parabelen beskriver punkter som er i lik avstand fra linjen x=-c og punktet F. Det betyr at hvis et punkt P=(x,y) flytter seg med tiden så er hastigheten vekk fra F og styringslinjen fra motsatt brennpunkt (c=-1) like store, dvs. d1=d2. Tangenten til parabelen blir diagonalen i parallellogrammet laget av de to komponentene i hastighetsvektoren.
Hvis parabelen er formet som et hulspeil vil stråler som kommer parallelt med x-aksen på figuren møtes i brennpunktet F.
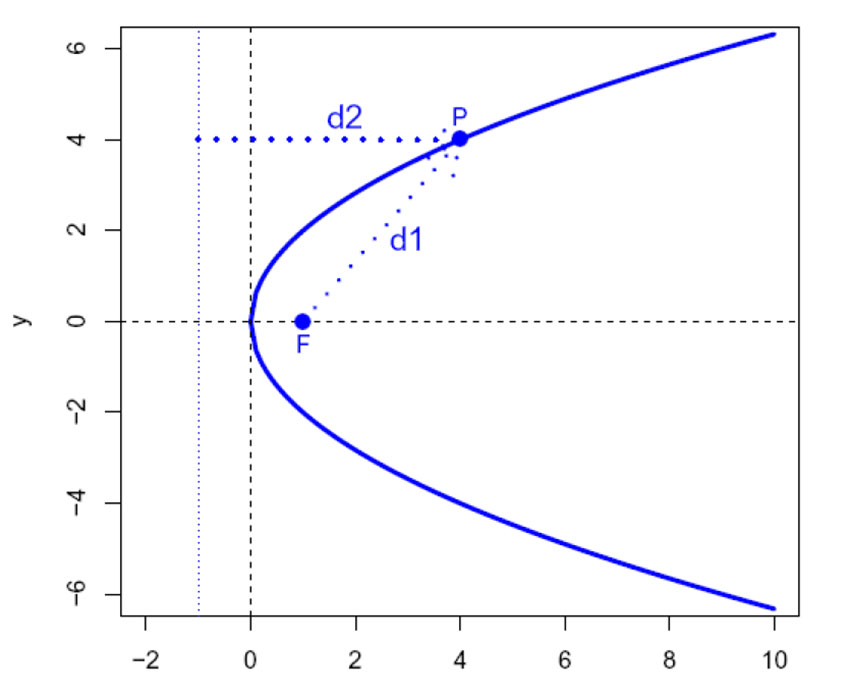
Funksjonen y2=4cx for c = 1. Punkt P(4,4) og brennpunkt F(1,0).
Generelt kan vi se på funksjonen:
\(f(x) =ax^2 + bx + c\)
Denne gir en parabel som har parabelakse parallelt med y-aksen, og fortegnet på a avgjør om den peker opp (a>0) eller ned (a<0). Løsningen av denne andregradsligningen gir røttene (nullpunktene i ligningen).
\(x=\displaystyle\frac{-b \;\pm\; \sqrt{b^2 - 4ac}}{2a}\)
Generelt kalles f(x)=xn for potensfunksjon med eksponent n. I Stefans lov er n=4.
Vi har det generelle integralet for potensfunksjoner (Wallis konjektur):
\(\displaystyle\int_0^a x^{\frac{p}{x}}dx=\frac{a^{(\frac{p}{q})+1}}{(\frac{p}{q})+1}=\frac{p}{p+q} a^{\frac{(p+q)}{q}}\)
Ellipse
En ellipse er punkter P=(x,y)som er like langt fra to fokalpunkter F1=(-c,0) og F2=(c,0) slik at avstanden d1=PF1 er like lang som d2=PF2, dvs. d1+d2=konstant.
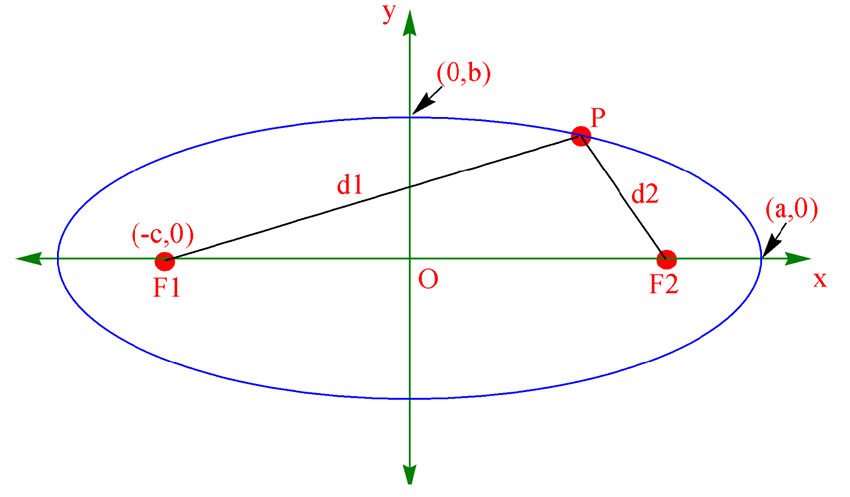
Ellipsen har den generelle formel:
\(\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Elilpsen ligger inne i et rektangel med bredde 2a og høyde 2b.
Forholdet mellom c/a kalles eksentrisiteten til ellipsen:
\(\displaystyle\frac{c}{a}=\sqrt{1-(\frac{b}{a})^2}\)
Eksentrisiteten ligger mellom 0 og 1. Hvis b er liten i forhold til a ligger fokalpunktene nær enden av x-aksen og ellipsen er lang og tynn med eksentrisitet nær 1. Etter hvert som b → a flyttes fokalpunktene mot sentrum i ellipsen som blir mer sirkelformet og eksentrisiteten nærmer seg 0.
\(d1=\sqrt{(a+c)^2+ y^2}\;\;\;\;\;d2=\sqrt{(x-c)^2 + y^2}\;\;\;\;\, |d1+d2|=2a\)
For ellipsen:
\(\displaystyle y=\sqrt{b^2 (1- \frac{x^2}{a^2})}\)
hvor a=8 og b=4
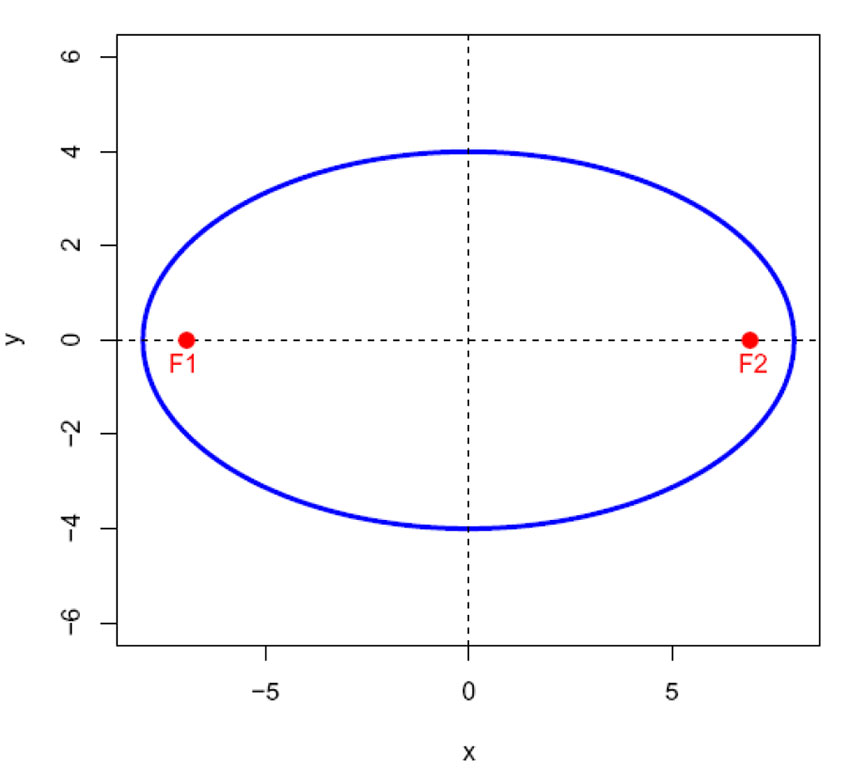
Arealet (A) av en sirkel er A=πr2 hvor r er radius. Lengden av omkretsen (O)av en sirkel, buelengden, er ==2πr. Hva blir det tilsvarende for en ellipse ?
Arealet (A) for en ellipse A er:
\(A=ab \pi\)
hvor a er halve lengden av x-aksen og b er halve lengden av y-aksen.
Vi kan plotte ellipsen på en annen måte, integrere og beregne arealet:
Buelengden av en ellipse var det vanskeligere å bestemme, og de som bidro til å finne ut av dette var Adrien-Marie Legendre (1752-1833) og Carl Gustav Jacob Jacobi (1804-1851). I buelengden (O) inngår det fullstendige elliptiske integral av andre type E:
\(O=4aE\)
hvor k er lik:
\(k= \sqrt{1-\frac{b^2}{a}}\)
og E er lik integralet:
\(\displaystyle E= \int_0^{\frac{\pi}{2}}\sqrt{1-k^2 \sin(\theta)}\;d\theta\)
Buelengden av en ellipse med a=8 og b=4 blir: 38.75379
Jorden har ellipseform grunnet sentrifugalkraften, radius av Jorden ved ekvator er a=6378.4 km og radius b over polene er 6356.9 km. Forskjellen i lengde i enn reise rundt Jorden langs ekvator og en reise gjennom polene blir ca. 67 km.
Johannes Kepler(1571-1630) fant at planetene fulgte elliptiske baner rundt Sola. Eksentrisiteten for banen til Jorden rundt Sola er 0.017.
I 1801 oppdaget italieneren G Piazzi asteroiden Ceres i bane mellom Mars og Jupiter, og deretter fant man flere store asteroider som Pallas, Juno, Vesta, Astrea, Hebe, Iris, Floris, Metis og Hygiea. Asteroidene beveger seg i samme retning som de store planetene, men eksentrisitet og helning av baneplanet varierer. Det var Gauss som fant hvor man måtte lete etter Ceres neste gang den dukket opp, vist i Theoria motus (1809). Målepunktene P(xi,yi)for Ceres som man hadde tilgjengelig plasserte Gauss i et elipseformet baneplan, og så beregnet han kjeglesnittet som passet best mulig overens med observasjonene ved å minimalisere de fem partiellderiverte i formelen for kjeglesnitt.
Hyperbel
I kjeglesnittet for hyperbel er |d1-d2|=konstant.
Den generelle formel for hyperbel er:
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Vi løser denne med hensyn på y:
\(y=\pm \frac{b}{a}\sqrt{x^2 - a^2}\)
Vi kan i tillegg trekke linjene y= ± bx/a som blir asymptotene til hyperbelen
Den konjugerte hyperbel er:
\(\frac{y^2}{b^2}-\frac{x^2}{a^2}= 1\)
\(y= \frac{b}{a}\sqrt{x^2 - b^2}\)
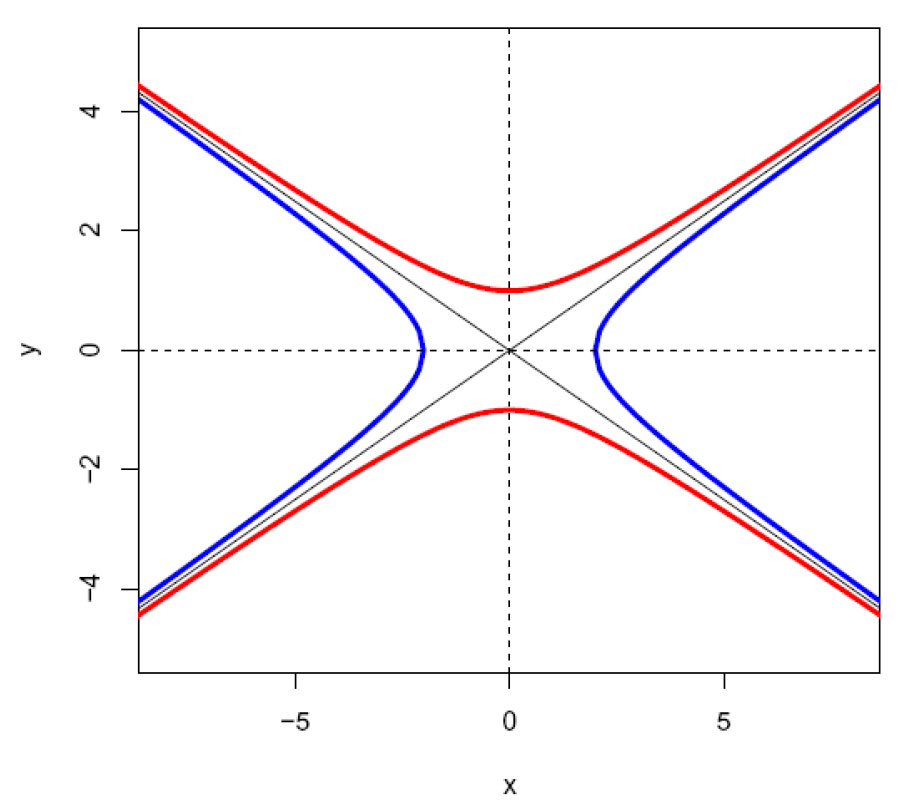
Hyperbel for a=2 og b=1, og den konjugerte hyperbel.
Polygonomskrivning
Start med en sirkel med radius for eksempel 2 cm. Omskriv sirkelen med en likesidet trekant. Omskriv trekanten med en sirkel. Omskriv sirkelen med en firkant. Omskriv firkanten med en sirkel. Omskriv sirkelen med en likesidet femkant (pentagon) (regulær mangekant). Omskriv pentagonet med en sirkel. Omskriv sirkelen med et heksagon, polygon hvor antall sider øker med 1 for hver gang, og omskriv med sirkler som foran. Rekkefølgen heksagon (6), heptagon (7), oktagon (8), nonagon (9), dodekagon (10), undekagon (11), dodekagon (12),osv. Hva vil til slutt radien i sirkelen bli hvis dette fortsetter ? Som man kan se av figuren er det en tendens til at radien etter hvert minsker i økning og gradvis nærme seg en grenseverdi.
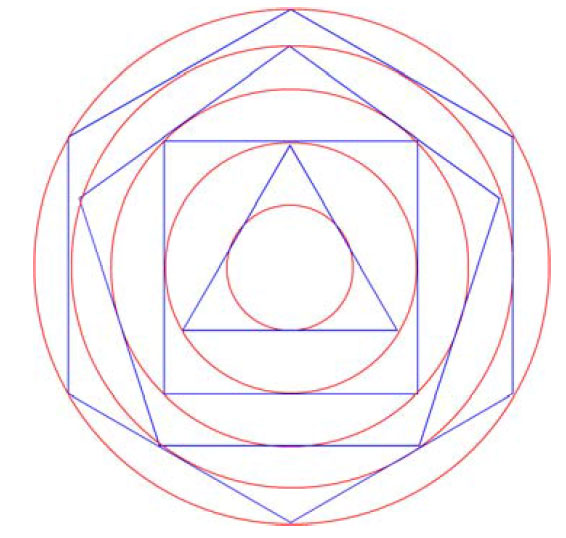
Grenseverdien r tilsvarer:
\(r= \frac{1}{(\cos \frac{\pi}{3}\cdot\cos \frac{\pi}{4} \cdot\cos \frac{\pi}{5}\cdot \dots)}\)
Alternativt kan dette skrives som:
\(\displaystyle r=\prod_{n=3}^{\infty}\frac{1}{\cos (\frac{\pi}{n})}\;\;\;\;\; \;r= \prod _ {n=3}^\infty \sec(\frac{\pi}{n})\)
Radien nærmer seg grenseverdien 8.7003662….
Radien rn+1 (n=1,2,…) til neste sirkel fra den foregående (rn) blir:
\(r_{n+1}=r_n\sec(\frac{\pi}{n+3})=r_n \frac{1}{\cos(\frac{\pi}{n+3})}\)
Vi kan også beregne radien av innskrevet (r) og omskrevet (R) sirkel til et polygon, her vist ved et pentagon. En omskrevet sirkel passerer gjennom alle hjørnene på polygonet. Lengden av sidekanten i polygonet er lik x. Radien av innskrevet sirkel (r) normalt ned på sidekanten deler x i to like deler (x/2). Vinkelen theta (θ) er vinkelen AOB og er lik:
\(\theta=\frac{360^o}{n}=\frac{2\pi}{n}\)
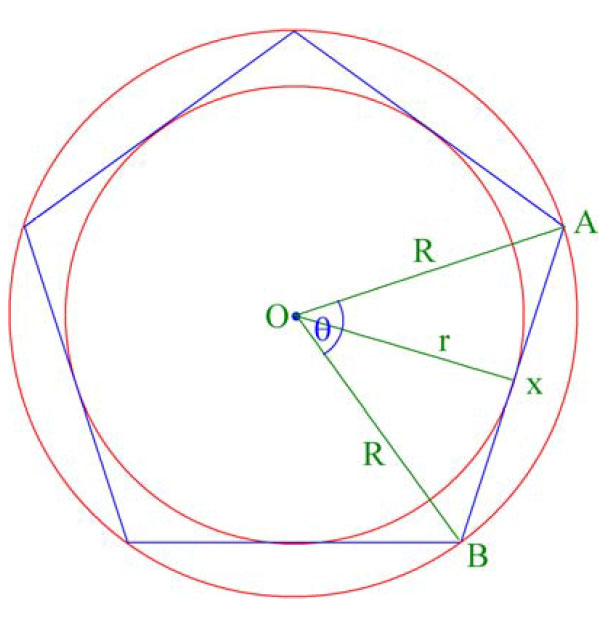
\(\tan(\frac{\theta}{2})=\frac{(\frac{x}{2})}{r}\;\;\;\;\; \sin(\frac{\theta}{2})=\frac{(\frac{x}{2})}{R}\)
\(r= (\frac{x}{2})\cot(\frac{\frac{\pi}{2}}{n})\;\;\;\;\;R= (\frac{x}{2})\csc(\frac{\frac{\pi}{2}}{n})\)
Arealet av trekanten AOB og hele polygonet:
\(\text{Areal AOB}=\frac{x}{2}r\;\;\;\;\; \text{Areal polygon}=n\frac{x}{2}r\)
Minner om:
\(\displaystyle \tan x=\frac{\sin x}{\cos x}\;\;\;\;\cot x=\frac{\cos x}{\sin x}=\frac{1}{\tan x}\;\;\;\; \sec x=\frac{1}{\cos x}\;\;\;\; \)
Når n blir stor nok nærmer arealet av polygonet seg arealet av en sirkel. Se hvordan Arkimedes fant en verdi for tallet pi (π) etter dette prinsippet.
Litteratur:
Apostol, T.M. Calculus (Vol I + II). Blaisdell Publ. Comp. 1962.
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.
Rottmann, Karl: Matematische Formelsammlung. Bibliographisces Insitutt. Hochschultaschenbücher-Verlag. 1960.