De triangulære tall er lik antall steiner i en trekant med n rader:

Dette blir tallene gitt ved:
\(\displaystyle\frac{1}{2}n(n-1)\)
De 20 første triangulære tallene i rekken:
1 3 6 10 15 21 28 36 45 55 66 78 91 105 120 136 153 171 190 210
En aritmetisk rekke får vi ved å addere til samme tall (k) til det foregående tallet, med start et gitt tall:
\(x_ {i+1}= x_i + k\)
Her starter rekken med 1 og legger til k=4 til det foregående:
1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81...
I en geometrisk rekke fra et starttall multipliseres hvert foregående tall med samme tall, noe som gir samme ratio:
\(x_ {i+1}= x_i \cdot k\)
Her starter man med 2 og ganger med k= 2:
2 4 8 16 32 64 128 256 512 1024 2048 ...
I en potensrekke opphøyes alle tallene i samme potens:
\(n^k \)
Her tallene n= 1-10 opphøyd i andre:
1 4 9 16 25 36 49 64 81 100
En kubisk rekke hvor hvert tall opphøyd i tredje, her n= 1-10:
1 8 27 64 125 216 343 512 729 1000
I en Fibonacci-rekke (Fibonaccitall) er et tall lik summen av de to foregående.
I en harmonisk rekke er hvert ledd et harmonisk middeltall mellom det foran og det etter. Et harmonisk middeltall X er den resiproke av gjennomsnittet av resiproke. Den resiproke betyr ”1 over…”
Den enkleste summen av en harmoniske rekken er:
\(1+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+ \dots \)
Collatz konjektur (formodning) (Lothar Collatz(1910-1990) starter med et tall. Hvis tallet er et liketall divider på 2 som blir det neste tallet i rekken. Hvis derimot tallet er et oddetall blir det nye tallet 3n+1. Dette lager en tallrekke som drifter opp og ned, haglstorm 3n+1, men uansett hvilket tall man starter med vil man komme på et eller annet tidspunkt vende tilbake til 1. Her et eksempel på starttall n=9
9 28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 4
Konvergerende rekker
På 1300-tallet fant den franske matematikeren og biskopen Nicole Oresme (ca.1325-1382) at delsummen av noen uendelig rekker konvergerer, det vil delsummene går mot en grenseverdi. Rekker som ikke går mot en grenseverdi divergerer.
\(\displaystyle\sum_{n= 1}^\infty \frac{n}{2^n}= \frac{1}{2}+ \frac{2}{2^2}+\frac{3}{2^3}+\dots= 2\)
Han fant også en annen rekke som konvergerer:
\(\displaystyle\sum_{n= 1}^\infty \frac{3n}{4^n}= \frac{3\cdot 1}{4^1}+ \frac{3 \cdot 2}{4^2}+\frac{3\cdot 3}{4^3}+\dots= \frac{4}{3} \)
Euler fant at det var en sammenheng mellom logaritmer og harmoniske rekker, publisert i De progressionibus harmonicis observationes(Observasjon om harmonisk progresjon) (1735).
\(\displaystyle\sum_{n= 1}^\infty \frac{1}{n}=\ln(n) + \gamma\)
Tallet gamma (γ) kalles Euler-Mascheronis konstant (Lorzenzo Mascheroni (1750-1800))
\(\gamma= \displaystyle \lim\limits_{n \to \infty}\left(\sum_ {k= 1}^n \frac{1}{k}- \ln(n)\right)= 0.5772156649015 \dots\)
Jakob Bernoulli ((1654-1705)) hadde arbeidet med sum i uendelige rekker, av typen (teleskoprekken), som konvergerer:
\(\displaystyle\sum_{n= 1}^\infty \frac{1}{\frac{n(n+1)}{2}}= 1+ \frac{1}{3}+\frac{1}{6}+\frac{1}{10}+\dots=2\)
Leonhard Euler (1707-1783) gjorde grunnleggende studier innen alle deler av matematikken: tallteori, geometri, algebra og kombinatorikk, publisert i Opera omnia. I Basel i Sveits hadde Euler Johann Bernoulli (1667-1748) som lærer, og Johanns sønn, Daniel Bernoulli(1700-1782) inviterte seinere Euler til St.Petersburg. Mye av det Euler skrev ble publisert i tidsskriftet til St.Petersburg Akademiet. Johann hadde også en bror, Jakob Bernoulli (1654-1705), onkel til Daniel, og dette Bernoulli-dynastiet hadde alle matematisk talent, men få har overgått Euler, selv ikke Gauss.
Rekkesummen nedenfor visste man at lå i nærheten av 8/5=1.6 (Basel-problemet), og Euler fant at rekken konvergerte mot π2/6= 1.644934... Nok et sted å treffe på tallet pi.
\(\zeta(2)= \displaystyle\sum_{n= 1}^\infty \frac{1}{n^2}= 1 + \frac{1}{4}+ \frac{1}{9}+ \frac{1}{16}+ \frac{1}{25}+ \frac{1}{36}+ \frac{1}{49}+\dots = \frac{\pi^2}{6}\)
I arbeidet med Basel-problemet fant Euler at følgende integral ble π/4:
\(\displaystyle\int_0^1 \frac{\sin(\ln(x))}{\ln(x)}= \frac{\pi}{4}\)
Euler tok som vanlig i bruk rekkeutvikling og kunne skrive:
\(\displaystyle\frac{\sin(\ln(x))}{\ln(x)}= \frac{\frac{\ln(x)^1}{1!}- \frac{\ln(x)^3}{3!}+ \frac{\ln(x)^5}{5!}- \frac{\ln(x)^7}{7!}+ \dots}{\ln(x)}= 1-\frac{\ln(x)^2}{3!}+\frac{\ln(x)^4}{5!}- \frac{\ln(x)^6}{7!}+ \dots\)
Euler fant også at følgende rekkesum konvergerer:
\(\zeta(4)= \displaystyle\sum_{n= 1}^\infty \frac{1}{n^4}= \frac{\pi ^4}{90}\)
I begynnelsen klarte ikke å finne ut om følgende rekkesum konvergerer, og eventuelt mot hva ?
\(\zeta(3)= \displaystyle\sum_{n= 1}^\infty \frac{1}{n^3}= 1 + \frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+\frac{1}{5^3}+ \dots= ?\)
ζ er Riemanns zetafunksjon, men i 1998 viste Roger Apéry (1916-1994) at rekkesummen er et irrasjonalt tall, 1.2020569032… kalt Apérys konstant
Euler arbeidet også med rekkene:
\(\displaystyle\sum_ {n= 1}^\infty \frac{1}{(2n-1)^2}= \frac{1}{2^2}+ \frac{1}{3^2}+ \frac{1}{5^2}+ \frac{1}{7^2}+ \dots= \frac{\pi^2}{8}\)
\(\displaystyle\sum_{n= 1}^\infty \frac{(-1)^{n+1}}{n^2}= \frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}- \frac{1}{4^2}+ \frac{1}{5^2}- \dots = \frac{\pi ^2}{12}\)
\(\displaystyle\sum_{n= 0}^\infty (-1)^n \frac{1}{(2n+1)^3}= 1- \frac{1}{27}+ \frac{1}{125}- \frac{1}{343}+ \dots= \frac{\pi^3}{2}\)
Følgende uendelige alternerende sum-subtraksjon er lik π/4:
\(\displaystyle 1 - \frac{1}{3}+ \frac{1}{5}- \frac{1}{7}+ \frac{1}{9}- \frac{1}{11} + \dots= \frac {\pi}{4}\)
Det naturlige tallet e er lik den uendelige summen:
\(\displaystyle\sum_ {n=0}^\infty= 1+ \frac{1}{1!}+ \frac{1}{2!}+ \frac{1}{3!}+ \frac{1}{4!}+ \dots= e\)
Den trigonometriske funksjonen sinus (x)kan uttrykkes som følgende rekkesum-substraksjon:
\(\sin(x) = \displaystyle x-\frac{x^3}{3!}+ \frac{x^5}{5!}- \frac{x^7}{7!}+ \frac{x^9}{9!}- \dots\)
Invers tangens (tan-1) eller atan(x) er lik:
\(\tan^{-1}x= \displaystyle x-\frac{x^3}{3}+ \frac{x^5}{5}- \frac{x^7}{7}+ \frac{x^9}{9}- \dots\)
\(\pi= \displaystyle 4 \left(\tan^{-1}\frac{1}{2}+\tan^{-1}\frac{1}{5}+ \tan^{-1}\frac{1}{8}\right)\)
Newton oppdaget den binomiale rekken:
\((1+x) ^k=\displaystyle\sum_{n= 0}^\infty \binom{k} {n}x^n = 1 + \binom{k}{1}x+ \binom{k}{2}x^2 + \binom{k}{3}x^3 + \dots\)
hvor binomialkoeffisientene:
\(\displaystyle\binom{k}{n}= \frac{k!}{n!(k-n)!}\)
Binomialkoeffisientene danner tallene i Pascals triangel.
Vi har for eksempel for k= 3 på den kubiske ligningen, og se at du finner igjen tallene i Pascals trekant:
\((1+x) ^3 = 1 + 3x + 3x^2+x^3\)
Hvis derimot k ikke er et positivt heltall får vi for eksempel k=-1:
\((1+x)^{-1}=\displaystyle \frac{1}{1+x}= 1 - x + x^2-x^3 + \dots \)
Det var denne som kunne gi Mercators rekke for logaritmefunksjonen:
\(\ln(1+x)= \displaystyle x- \frac{x^2}{2}+ \frac{x^3}{3}- \frac{x^4}{4}+ \dots \)
Hvis k=1/2 får vi:
\(\displaystyle (1+x) ^{\frac{1}{2}}= \sqrt{1+x}= 1+\frac{1}{2}x- \frac{1}{8}x^2+ \frac{1}{16}x^3- \dots\)
Hvis en funksjon f(x) kunne utvides til en uendelig potensrekke:
\(f(x)= b_0 + b_1 x + b_2 x^2+ b_3 x^3 + \dots= \displaystyle\sum_{n= 0}^\infty b_ n x^n\)
så vil den deriverte av rekken f´(x) bli:
\(f'(x)= b_1 + 2b_2 x+ 3b_3 x^2 + \dots= \displaystyle\sum_{n= 0}^\infty nb_ n x^{n-1}\)
John Wallis (1616-1703)som skrev i 1655 Arithmetica infinitorium (Aritmetikk om det uendelige) hadde funnet den berømte uendelige produktrekken for pi (π):
\(\displaystyle\frac{\pi}{2}= \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \dots\)
Alternerende rekker og Cesàrosummering (C,n)
Alternerende rekker er rekker på formen:
\(\displaystyle\sum_{n=0}^\infty (-1)^n a_n \;\;\;\;\;\,\text{hvor} \;\;a_n>0\)
Hvorvidt en slik rekke konvergerer kan undersøkes med Leibniz test, som sier at hvis grensen for sekvensen an er lik 0 når n går mot uendelig (∞), det vil si at sekvensen an er monotont minskende, og rekken konvergerer.
Følgende alternerende harmoniske rekken konvergerer. Vi viser det med Leibniz test hvor an=1/n går mot 0 når n går mot uendelig:
\(\displaystyle 1 - \frac{1}{2}+ \frac{1}{3}- \frac{1}{4}+ \frac{1}{5}- \dots= \ln2\)
Man kan lage en rekke av de naturlige heltallene og skifte fortegn alternerende
\(1-2+3-4+5-6+7-\dots\)
\(\displaystyle\sum_{n= 1}^\infty n(-1) ^{n-1}\)
Intuitivt vil vi si at denne rekken divergerer, allikevel skrev Euler at denne rekken konvergerer mot 1/4. Tallene i rekken
1 -2 3 -4 5 -6 7 -8 9 -10 11 -12 13 -14 15 -16 17 -18 19 -20 21 -22 23 -24 25 -26 27 -28 29 -30
Vi ser nærmere på den og hvorfor Euler hadde rett:
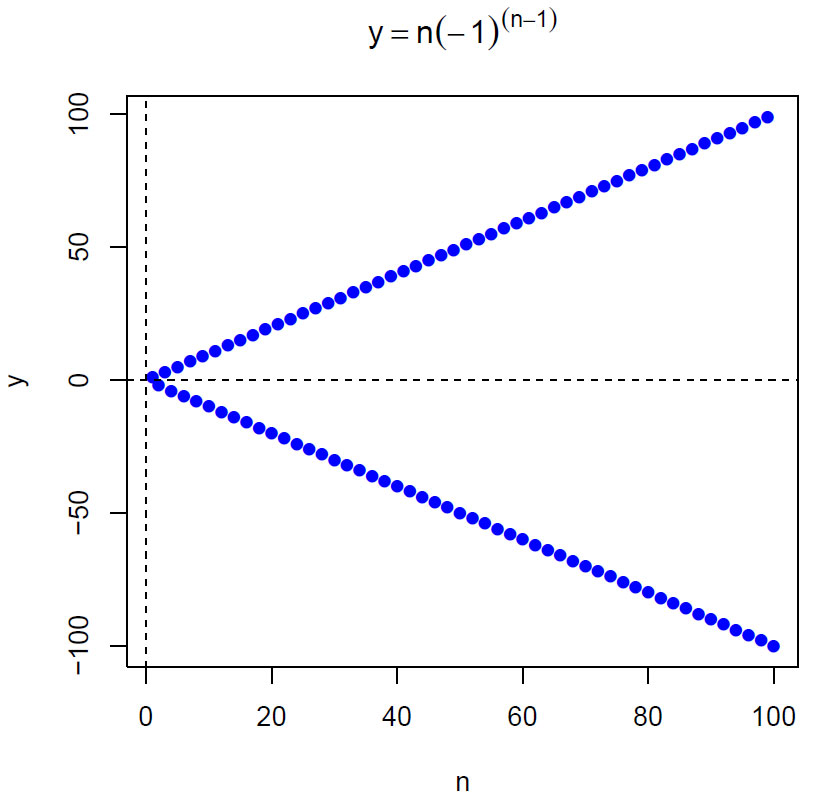
I figuren foran ser vi på enkelttallene i rekken, nå kan vi se på delsummen av rekken ved å la n gå fra 1-100. Summene når n går fra 1 og øker blir 1,-1,2,-2,3,-3,….
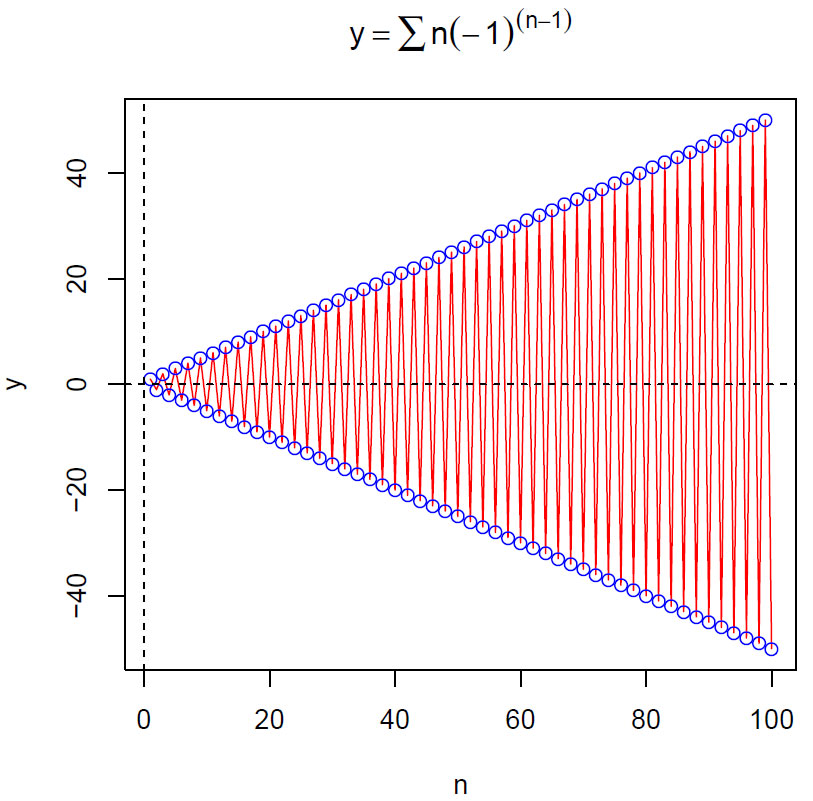
Vi ser at summen av 100 ledd i rekken blir 50 , og -50 og det virker paradoksalt at denne summen skal bli lik 1/4.
Summene når n går fra 1 og øker blir 1,-1,2,-2,3,-3,….
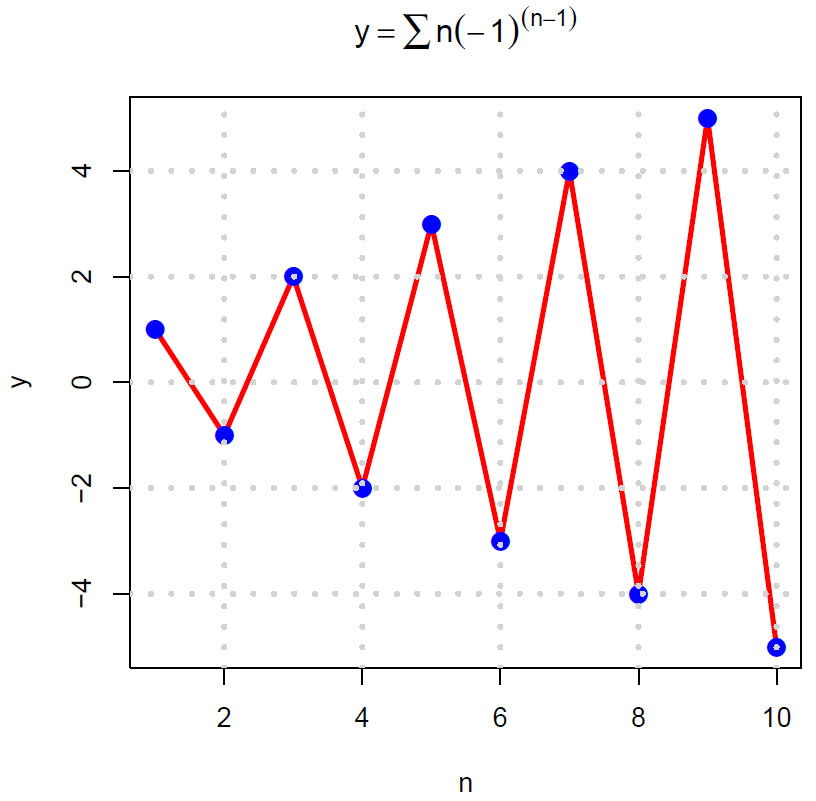
Ernesto Cesàro (1859-1906) studerte denne summen nærmere, og den er en spesialutgave av følgene rekke, noe også Euler oppdaget:
\(1- 2^n+3^n-4^n+ 5^n- \dots\)
Hvis n= 1 blir denne rekken:
1 -2 3 -4 5 -6 7 -8 9 -10 ...
Hvis n= 0 blir rekken:
1 -1 1 -1 1 -1 1 -1 1 -1 ...
Hvis n= 2 blir rekken:
1 -4 9 -16 25 -36 49 -64 81 -100 ...
Rekken 1-1+1-1+… kalles Grandis rekke, (italiensk matematiker Guido Grandi) som divergerersom det kan argumenteres for konvergerer paradoksalt mot Cesàrosum 1/2, foreslått av Euler.
Grandis uendelig rekke:
\(\displaystyle\sum_ {n= 0}^\infty (-1)^n= 1-1+1-1+1-1+ \dots\)
Dette er også lik Dirichlets etafunksjon η(0)=0.5
η(-1)=0.25
η(-1) blir lik 1/4, det samme som Cesàro summen av
\(\displaystyle\sum_{n= 1}^\infty n(-1)^{n-1}\)
Sekvensen av delsummer blir 1,0,1,0,…, og denne rekken konvergerer ikke.
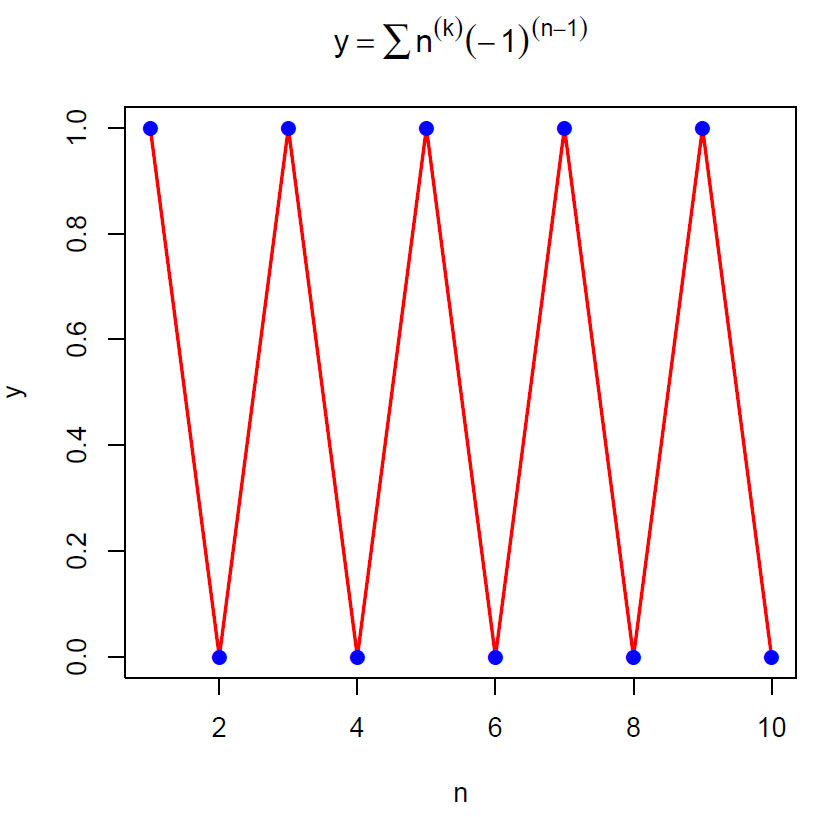
Siden de nevnte rekker er tall som summeres kan man manipulere med rekkefølgen av tallene i summasjonen. Gjennomsnittene av delsummene av rekken 1-2+3-4+5-… blir:
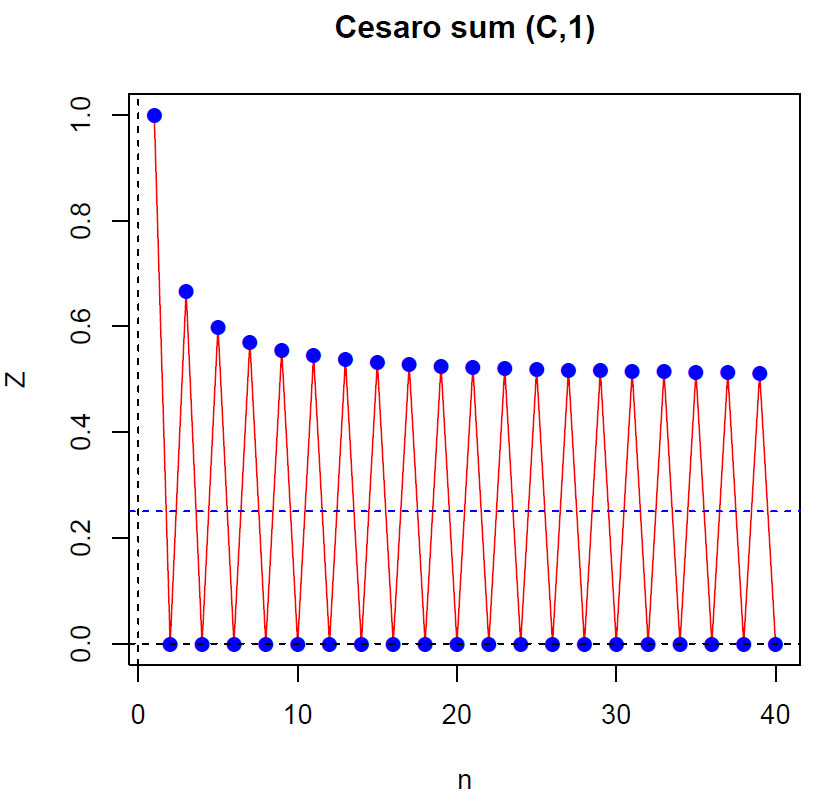
Vi kan se at Grandisrekken er Cesàrosummerbar og konvergerer mot en 1/2:

Vi kan regne ut gjennomsnittene av delsummene som blir rekken
1, 0, 2/3, 0, 3/5, 0, 4/7,… men vi ser at denne rekken ikke konvergerer som betyr at den er ikke Cesàrosummerbar. Derimot kunne Otto Hölder vise at vi Höldersummering (H,n) og Cesàrosummering (C,n) gir samme resultat. Hvis vi tar snittene av gjennomsnittene (C,2) ser vi at summen konvergerer mot 1/4.
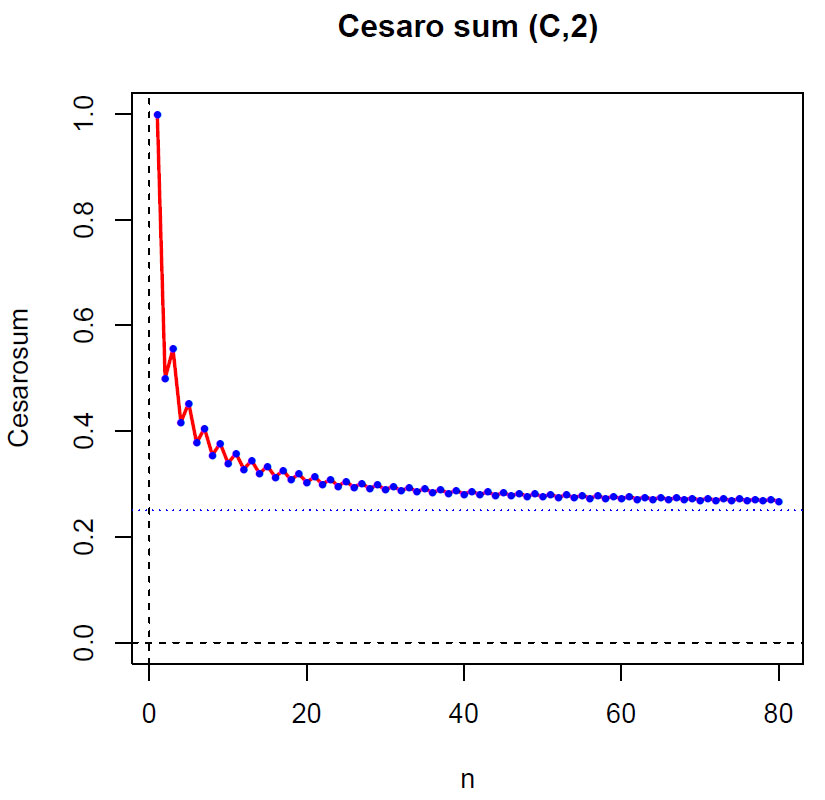
Cesàrosummering av uendelige rekker vil generelt si at har man rekken:
\(\displaystyle\sum_{n= 1}^\infty x_n\)
med delsummen sk for det k-te element:
\(s_k= x_1 + x_ 2 + x_3+ \dots +x_k\)
så vil rekken være Cesàrosummerbar hvis delsumrekken konvergerer mot en sum A:
\(\displaystyle\lim\limits_{n \to \infty}\frac{1}{n}\sum_ {k= 1}^n s_k = A\)
For Grandisrekken ser vi at partialsummene konvergerer ikke, men det gjør gjennomsnittet av delsummene 1/1,1/2,2/3,2/4,3/5,3/6,…
\(\displaystyle\lim\limits_{n \to \infty} \frac{s_1 + s_ 2 + s_3+ \dots + s_n}{n} \)
som blir lik 1/2.
Vi kan uttrykke Cauchy-produktet av to uendelige rekker (Augustin Louis Cauchy (1789-1857) og i vårt tilfelle med produktet av to Grandisrekker har vi:
\(\displaystyle c_n = \sum_{k=0}^n a_k b_{n-k}= \sum_{k=0}^n (-1)^k(-1)^{n-k}= (-1) ^n (n-1)\)
Vi ser nå at n starter ved 0, men vi får samme resultat som tidligere, og ser at produktet av to Grandisrekker blir lik rekken 1, -2, 3, -4, 5, -6 ...
1 -2 3 -4 5 -6 7 -8 9 -10 11 ...
Det er også en nær tilknytning til Abelsk summering.
Dessuten ser man likhetstrekk med absurde summer man får ved bruk av Riemanns zeta-funksjon. Se også Dirichlets etafunksjon.
Euler fant også konvergering av rekken:
\(\displaystyle 1-2x+3x^2-4x^3+5x^4+ \dots= \frac{1}{(1+x)^2}\;\;\;\;\;\; \text{for }\;\; |x|<1\)
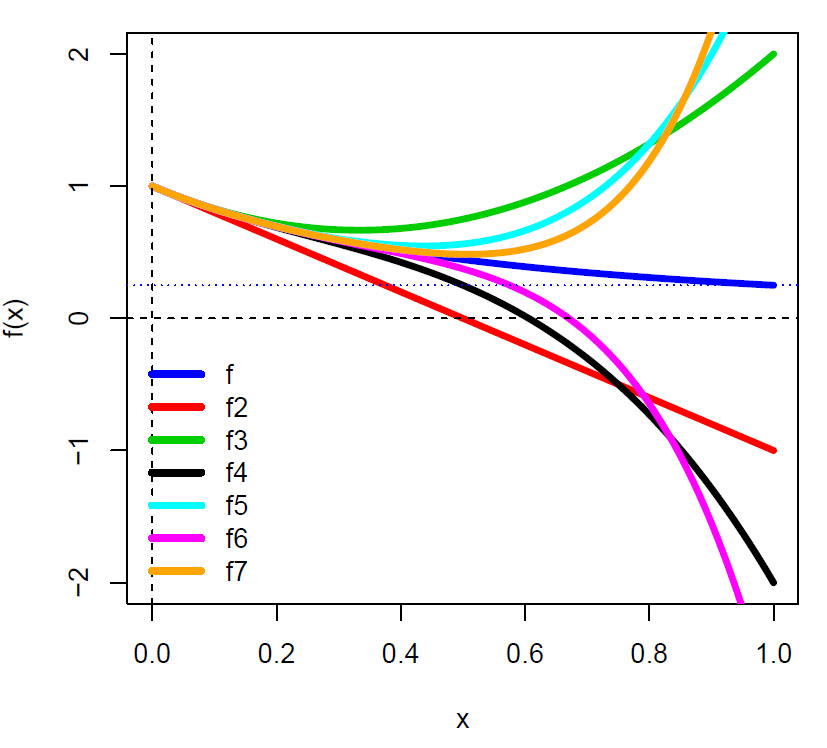
Figuren viser funskjonene:
\(\displaystyle f= \frac{1}{(1+x) ^2}\)
\(\displaystyle f2=1-2x \)
\(\displaystyle f3=1-2x + 3x^2\)
\(\displaystyle f4=1-2x + 3x^2-4x^3\)
\(\displaystyle f5=1-2x + 3x^2-4x^3 + 5x^4\)
\(\displaystyle f6=1-2x + 3x^2-4x^3 + 5x^4-6x^5\)
\(\displaystyle f7=1-2x + 3x^2-4x^3 + 5x^4-6x^5+ 7x^6\)
Ved x=-1 konvergerer 1/(1-x)2 ved 1/4.
Vi har også den abelske summen:
\(\displaystyle \lim\limits_{x \to -1}\sum_ {n= 1}^\infty n(-x)^{n-1}= \lim\limits_{x \to -1} \frac{1}{(1+x) ^2}= \frac{1}{4}\)