Terningkast

Et terningkast

\(\displaystyle P\left( X=x_i\right)=\frac{1}{6} \space \space x_i \in \left\{ 1, 2, 3, 4, 5, 6\right\}\)

Sannsynligheten for å kaste en treer er P(X = 3) = 1/6. Sannsynligheten for å få en sekser i et terningkast er P(X = 6) = 1/6. X er en diskret (diskontinuerlig) stokastisk (tilfeldig) variabel som representerer alle mulige utkomme av et terningkast, et stokastisk eksperiment. Variabelen X har ingen enkeltverdi, men har en statistisk diskret sannsynlighetsfordeling av verdier.

P(X = x_i) betyr sannsynligheten for at den tilfeldige variabelen X skal ha verdien x_i, hvor x_i er et tall i utfallsrommet. En hendelse kan ikke samtidig både skje og ikke skje, de utelukker hverandre gjensidig. Når terningen kastes er alle utfall uavhengige av hverandre.

Legg merke til at på en vanlig spillterning blir summen av øyne på to motsatte sider alltid lik 7.

Simulering av n=100000 kast av en vanlig spillterning i R. Utfallet følger en uniform sannsynlighetsfordeling, hvor sannsynligheten for hvert av utfallene er lik 1/6 = 0.1666..

Sannsynligheten for at hendelse A skal skje, P(A) eller Pr(A), er lik brøken antall måter man kan få hendelse A  (=suksess) dividert på det totale utfallsrommet S som inneholder antall mulige utkomme.

\(\displaystyle P\left(A\right)=\frac{\text{gunstig utfall }}{\text{mulige utfall}}\)

Den komplementære hendelsen \(P(\overline A)\), at A ikke skjer, blir:

\(\displaystyle P\left (\overline A\right)=1-P\left(A\right)\)

Sannsynlighetsteori er studiet av tilfeldige utkomme i et eksperiment. Tilfeldig (stokastisk) betyr at utkomme ikke er fastlagt på forhånd,  det er innebygget en usikkerhet i eksperimentutfallet. Sannsynlighet og mengdelære har samme logiske struktur.

Sannsynlighet P som befinner seg i intervallet [0 , 1] er en tellbar egenskap som tilhører en samling undermengder (delmengder) av en universell mengde, det totale utfallsrommet S. Den totale sannsynlighet er lik 1, P(S) = 1, og sannsynligheten kan aldri være større enn 1.

Den diskrete variabelen X for et terningkast er uniformt fordelt og summen av sannsynlighetene blir lik 1:

\(\displaystyle \sum_{i=1}^{6}P\left(X=n\right)=1\)

Vi ønsker å uttrykke sannsynligheten for en hendelse (event) i S. Sannsynlighet har en analogi med en masse = 1 som kan bli fordelt i varierende tykkelse over et område på den reelle tall-linjen. Noen steder på aksen tall-linje plasserer man mye av massen, på andre deler lite eller ingenting. Der hvor man har plassert mest masse blir det størst sannsynlighet. Dette gjenspeiles i begrepet sannsynlighetstetthetfunksjon. Hvis det ikke er noen skjevhet i uttaket av prøver fra S så vil punktsannsynligheten P(x_i) være lik for alle elementene (objektene) x_i i S. Sannsynligheten for å få to seksere i to terningkast er 1/6² = 1/36. Dette er to uavhengige hendelser hvor sannsynligheten følger multiplikasjonsregelen. Sannsynligheten for å få tre seksere i tre terningkast er 1/6³=1/216.Sannsynligheten for ikke å få en sekser i et terningkast er 1-P(X = 6) = 5/6. Vi kan også betrakte det å få en 6er og alternativt ikke en 6er som en binomial sannsynlighetsfordeling. Sannsynligheter kan visualiseres med Venn-diagram.

Forventningsverdi  E(X) for en diskret stokastisk variabel for et terningkast med seks mulige utfall er:

\(\displaystyle E\left(X\right)= \sum_{i=1}^{6}x_iP\left(X=x_i\right)\)

Du får ikke 3.5 ved å kaste en terning, men det er et veiet gjennomsnitt (middelverdi µ).

Jo større variansen er desto mindre sannsynlig er det å treffe på forventningsverdien.

Varians Var(X) for en diskret stokastisk variabel er:

\(Var\left(X\right)= E\left( \left( x-E\left(X\right)\right)^2\right)\)

\(Var\left(X\right)=\sum_{i=1}^{6}\left[x_i-E\left(X\right)\right]^2\cdot P\left(X=x_ i\right)\)

\(Var\left(X\right)=E\left(X^2\right)-\mu^2\)

\(E\left(X^2\right)=\sum_{i = 1}^{6}P\left(X=x_ i\right)\)

Sannsynligheten for at en terning viser 4,  5 eller 6 blir:

\(\displaystyle P\left(4\leq X \leq 6\right)=\sum_{i=4}^{6}P\left(X=x_i\right)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}\)

Hva er sannsynligheten for å få et liketall eller et multiplum av 3 (delelig på 3) ved å kaste en terning?

Vi har undermengden liketall:  A = {2,  4,  6}  fra utfallsmengden S, og undermengden multiplum av 3, delelig på 3:  B = {3,  6}. Vi er interessert i unionen AUB = {2,  3,  4,  6}. Union (U) tilsvarer logisk og. Snitt (\(\cap\)) tilsvarer logisk eller. P(AUB) = 4/6  = 2/3,  fordi unionen har 4 elementer. Vi kunne også ha regnet ut på en annen måte:

\(\displaystyle P\left(A \cup B\right)=P\left(A\right) + P\left(B\right)-P\left(A\cap B\right)=\frac{3}{6 }+\frac{2}{6}-\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)

Sum av to terninger

Utfallsrommet for summen av antall øyne på for de sidene som vender opp ved kast av to rettferdige terninger er S= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Følgende 6x6 matrise viser mulige utfall for summen av to terninger. Antall mulige utfall ved kast av to terninger  er lik 36  (6²):

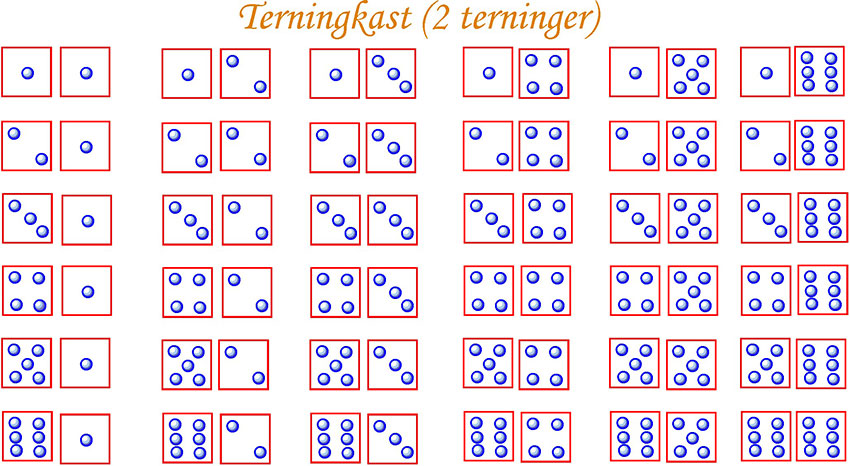
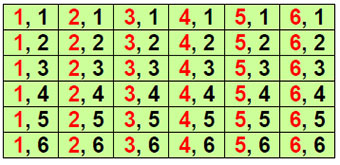
Punktsannsynlighetene for summering av ”øyne” på to terninger

blir:

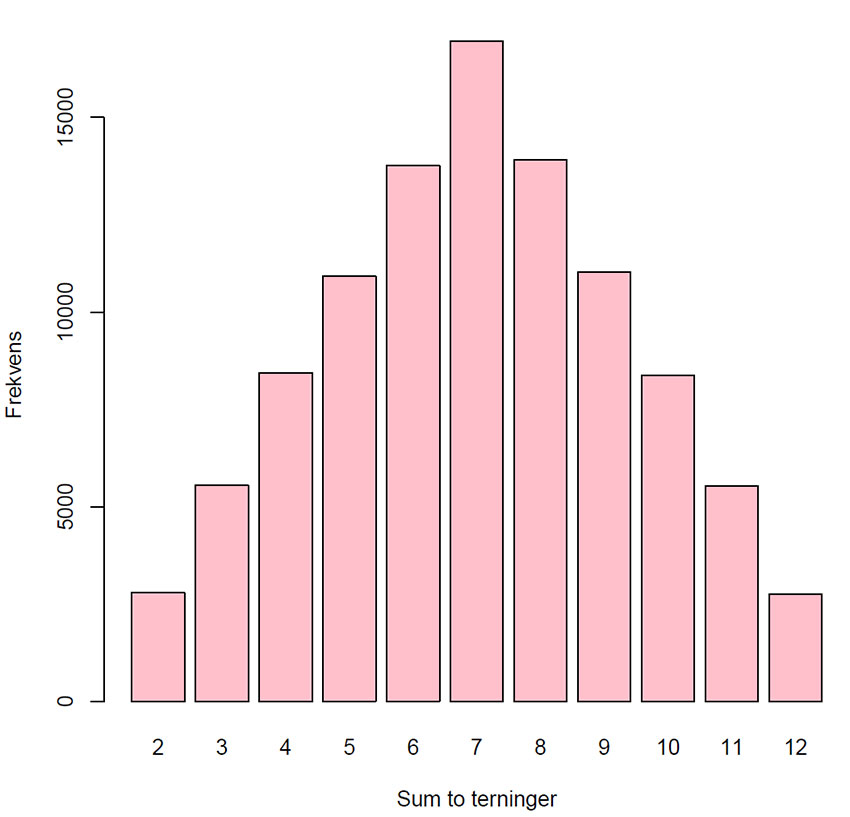
Stolpediagram av simulert eksperiment med n=100000 kast av to terninger, og beregning av summen av antall "øyne "som vender opp. Forventet verdi E(X)=7 og varians Var(X)=5.8.

Histogram fra simulering av n=100000 kast med to terninger og beregning av summen av dem. De samme punktsannsynlighetene man finner i tabellen ovenfor.

\(E\left(X\right)=\sum_{i=2}^{12}x_iP\left(X=x_i\right)\)

hvor x_i er utfallene i utfallsrommet S= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, og  P(X=x_i) er sannsynlighetene for de forskjellige utfallene vist i tabellen over.

Varians er lik:

\(Var\left(X\right)=\sum_{i=2}^{12}\left(x_i-E\left(X\right)\right)^2\cdot P\left(X=x_i\right)\)

Sum av tre terninger

Utfallsrommet S ved sum av tre terninger er

S = {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18}

Det er 6³=216 mulige utfall ved kast av tre terninger. Det er det samme om en terning kastes tre ganger eller tre terninger en gang hvis det ikke er noen interaksjon mellom terningene. Sannsynligheten for hvert av disse utfallene er1/216.
Alle mulige kombinasjoner for summen ved kast av tre terninger er 6³=216. Sum av 4 terninger gir 6⁴=1296 kombinasjoner osv.

Stolpediagram fra simulering av en million kast av tre terninger og beregning av summen av øyne på siden som vender opp.

Det er bare en måte å få sum 3 = 1+1+1 og en måte sum 18 = 6+6+6

Histogram av simulering av n=1000000 kast med tre terninger og beregning av sum av dem

Utfall for sum av tre terninger.

Triangulære tall

Triangulære tall angir hvor mange måter heltallet N kan skrives som summen av tre positive tall. Eksempler på triangulære tall er 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, …Vi ser at dette gjelder for sum av tre terninger opp til utkomme 21.

Et triangulære tall T_n

\(T_n=\sum_{k=1}^{n}k=\frac{n\left(n+1\right)}{2}\)

1   3   6  10  15  21  28  36  45  55  66  78  91 105 120 136 153 171 190

Summen av to på hverandre følgende triangulære tall er et kvadrattall.

For tabellen over er for  n>8 er det ikke lenger triangulære tall. Tallet 9 kan skrives som 1+1+7,  1+7+1,  7+1+1,  men siden terningen stopper ved tallet 6 følger ikke rekken lenger de triangulære tallene,  men symmetrien kommer tilbake igjen for n >12. 

de Méré og gambling

Kaster man to terninger{a,b}, hver med mulige utfall {1,2,3,4,5,6} så blir prøverommet for to terninger

S={6²=36 mulige utfall}={x₁, x₂ ,x₃,…, x₃₆}. Punktsannsynligheten for hvert utfall er 1/36=1/6∙1/6. For to uavhengige hendelser A og B har vi snittet for sannsynligheten P for de to hendelsene P(A) og P(B):

\(\displaystyle P(A \cap B)= P(A) \cdot P(B)\)

Hva er sannsynligheten for minst en dobbel sekser ved kast av to terninger n ganger ? Det var dette problemet Chevalier de Méré presenterte for Blaise Pascal, som igjen kontaktet Fermat om problemet. Lønner det seg å satse på et veddemål på minst to seksere i 24 kast ? To spillere fått et avbrudd i et sjansespill om en angitt poengsum. Hvis poengsummen er gitt, hvordan fordele pengene ? Huygens skrev  De ratiociniis in ludo alea (Om regning og sjansespill) i 1657, basert på  brevvekslingen mellom Pascal og Fermat. Dette er statistikkens begynnelse hvor begrepet forventning dukker opp.

Sannsynligheten for en dobbel sekser i n kast er (1/36)ⁿ

Sannsynligheten for ingen dobbel sekser i n kast er (35/36)ⁿ.

Hvis de Méré skulle få en sannsynlighet på over 50% på å få en dobbel sekser i n kast, hvor mange ganger måtte han kaste ? de Méré var i utgangspunktet usikker på om 24 kast var nok, og at dette var i grenseområdet for tvil ser man av regnestykket nedenfor

Vi kan sette opp regnestykket, hvor vi heller ser på sannsynligheten for ikke få en dobbel sekser:

\(\displaystyle 1- \left(\frac{35}{36}\right)^n>\frac{1}{2}\)

eller:

\(\displaystyle \left(\frac{35}{36}\right)^n<\frac{1}{2}\)

Vi tar logaritmen på begge sider:

\(\displaystyle n \ln 35-n\ln 36 <-\ln2 \;\;\;\,\; \implies\;n< \frac{\ln 2}{\ln 36-\ln35}=24.6051\)

Det vil si at sannsynligheten er p<1/2=50% når n=24 kast og p>1/2 når n≥25 kast

Litteratur

R Core Team (2016). R: A language and environment for statistical
  computing. R Foundation for Statistical Computing, Vienna, Austria.
  URL https://www.R-project.org/.

Wikipedia

Natur og kultur

Alea iacta est – terningen er kastet, ifølge historien uttalt av Julius Cæsar da han krysset elven Rubicon pr 49 f.kr  som ga starten av den store romerske borgerkrigen. Betyr den endelige avgjørelsen er fattet.

Tilbake til hovedside