Ved kast av en rettferdig mynt tilsier erfaring, fornuft og intuisjon at hvert kast er uavhengig av det forrige. Utfallet av et kast påvirker ikke utfallet av neste kast, og sannsynligheten for å få kron er 50% (½), men dette gjelder bare hvis man foretar svært mange kast (De store talls lov). Andelen av kron vil ved mange kast konvergere mot 0.5.

Femtiøringen er gått ut av bruk, men er praktisk til eksperimenter med myntkast. Mynt: Revers(bakside) fabeldyr fra Urnes stavkirke. Kron: Advers (forside)
Vi kan ikke si noe om utfallet av variabelen X som sådan, men vi kan si noe om sannsynligheten. Vi lar utfallet kron være lik 1 og utfallet mynt lik 0
\(P(X=1)=P(X=0) = \frac{1}{2}\)
Summen av sannsynlighetene er lik 1.
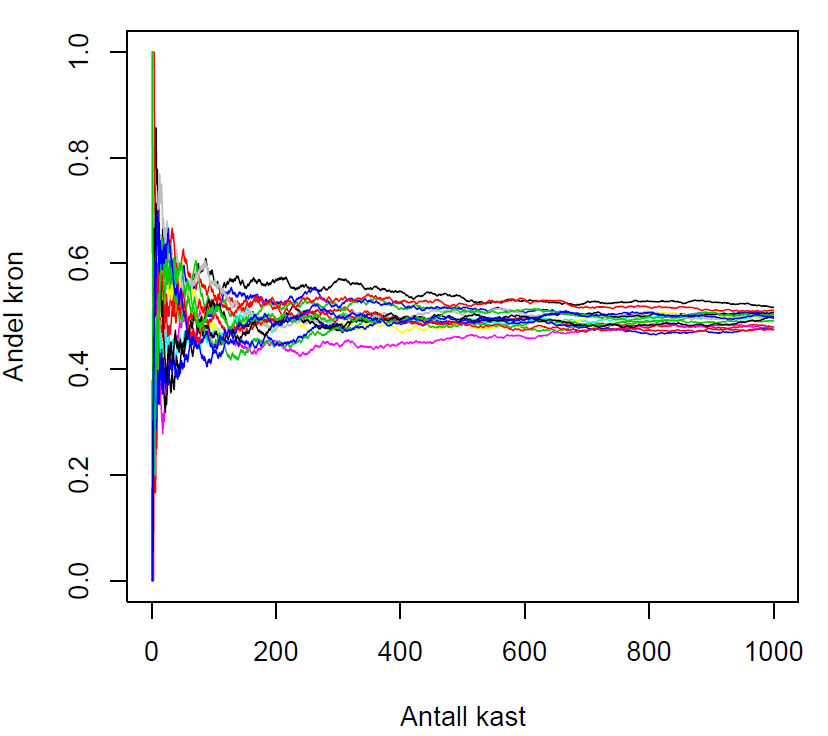
Simulerte myntkast. Etterhvert nærmer sannsynligheten seg 0.5 for antall kron.
Vi har en diskret stokastisk (tilfeldig) variabel X som angir antall kron ved kast av et pengestykke (50-øring). Variabelen X er en funksjon som i et myntkast gir eller tilordner et reelt tall. Ved kast av en mynt blir verdimengden til funksjonen X som angir antall kron lik {1, 0}, det vil si en kron eller ingen kron, altså to utfall (21).
Utfallsrommet for ett myntkast er:
S = {k, m} hvor k=kron og m=mynt
Utfallsrommet ved kast av to mynter er inneholder fire mulige utfall, 22:
S= {kk, km, mk, mm}
I dette tilfellet blir verdimengden til den stokastiske funksjonen X lik {0, 1, 2} kron.
Utfallsrommet ved kast av tre mynter som inneholder åtte mulige utfall, 23:
S= {kkk. kkm, kmk, mkk, kmm, mkm, mmk, mmm}
Verdimengden for funksjonen X blir i dette tilfellet {0, 1, 2, 3 } kron,

Bernoullifordelingen
Oppkalt etter den sveitsiske matematikeren Jacob Bernoulli, er en diskret sannsynlighetsfordeling med bare to utkomme (dikotome utfall): suksess - ikkesuksess, kron - mynt, 1 versus 0, riktig - galt, tilstede - fraværende, ja – nei, reproduksjon-ikke reproduksjon osv. Bernoullifordelingen er et spesialtilfelle av den bionomiale fordelingen hvor n=1.

Sveitsisk frimerke Jacob Bernoulli.
Gjentatte myntkast er en sekvens av eksperimenter utført under samme betingelser. Myntkastene er uavhengig av hverandre. Utkomme av et kast er ikke påvirket av utfallet av det forrige. De to sannsynlighetene p og q blir henholdsvis for suksess (X = 1 = kron (k)), hvor 0 ≤ p ≤1:
\(P(X=1)= p\)
For ikkesuksess (X = 0 = mynt(m))
\(P(X=0)=q= 1-p\)
p for x(1) suksess og sannsynlighet q = 1-p for x(0) ikke-suksess. hvor 0 ≤ p ≤1. For myntkast har vi P(kron) = p, og P(mynt) = 1-p = q.
Bionomial sannsynlighetsfordeling
Utfallet av en rekke Bernoulli-eksperimenter følger en Binomial sannsynlighetsfordeling.
For en binomial fordeling er sannsynligheten for suksess k ganger i n uavhengige forsøk P(X = k) lik:
\(\displaystyle P(X=k)= \frac{n!}{(n-k)!k!}\;p^kq^{n-k}=\binom{n}{k}p^kq^{n-k}\;\; \;k=0, 1, 2, 3,...,n\)
uttrykt som binomialkoeffisienter
\(\displaystyle\frac{n!}{k!(n-k)!} = \binom{n}{k}\)
Binomialkoeffisienter n over x gir Pascals trekant.
Fakultetsfunksjonen n! (n fakultet) er gitt ved:
n! = n(n-1)(n-2)...3·2·1
0! = 1, det er bare en måte å ordne null objekter.
Fakultetsfunksjonen gjelder bare for positive heltall. Det er bare når n=0 og n=1 at n! blir et oddetall, ellers blir det alltid et liketall, og den øker meget raskt med økende n. For eksempel for tallene n=0-10:
1 1 2 6 24 120 720 5040 40320 362880 3628800
Fakultetsfunksjonen kan også uttrykkes som produktnotasjon:
\(\displaystyle n!=\displaystyle\prod_{k=1}^nk\)
Summen av alle punktsannsynlighetene, det vil si fordelingsfunksjonen F(x), som er den kumulative sannsynligheten for k suksess i n forsøk:
\(F(x)= \displaystyle\sum_{k=0}^{n} P(X=k)=\displaystyle\sum_{k=0}^{n}\binom{n} {k}p^kq^{n-k}=\left(p+q\right)^n=1 \)
Fordeling ved å kaste 1 mynt: (p+q)1
Fordeling ved å kaste 2 mynter: (p+q)2
p2 + 2pq + q2 = 1
Fordeling ved å kaste 5 mynter: (p+q)5
p5 + 5p4q + 10p3q2 + 10p2q3 + 5pq4+q5
Legg merke til koeffisientene 1 5 10 10 5 1 fra Pascals trekant.
Sannsynlighet for 5 kron ved kast av fem mynter : (1/2)5 = 1/32 = ca. 3%
Eller hvis man vil uttrykke det som utfall kron (k) eller mynt ved å kaste 5 mynter: (k+m)5
k5 + 5k4m + 10k3m2 + 10k2m3 + 5km4 + m5
Generelt uttrykt via binomialkoeffisientene:
\(\left(a+b\right)^n=\displaystyle\sum_ {k=0}^n \binom{n}{k}a^kb^{n-k}\)

Sannsynligheten for de forskjellige utfall for antall kron ved kast av fem mynter.
Forventning E(X) for en binomial fordeling er:
\(E(X)=np\)
Varians Var(X) for en binomial fordeling:
\(Var(X)=npq=np(1-p)\)
Forventet antall kron (suksess) i 5 kast:
\(E(X)=np=5 \cdot 0.5=2.5\)
Vi kan også sjekke dette ved å summere produktet av k kron i n forsøk og punktsannsynlighetene, dvs. n=5, k kan ha utfallene 0, 1, 2, 3, 4 eller 5 med sannsynlighetene P(X=k) henholdsvis 0.03125 0.15625 0.31250 0.31250 0.15625 0.03125. Summen av disse sannsynlighetene blir lik 1.
\(E(X)=\displaystyle\sum_{k=0}^{n}kP\left(X=k\right)=\displaystyle\sum_{k=0}^{n}k\binom{n} {k}p^kq^{n-k}=np \)
Etter hvert som n øker vil den binomiale fordelingen (diskontinuerlig) bli mer lik normalfordelingen (kontinuerlig).
Forventningen til en diskret stokastisk variabel er:
\(E(X)=\displaystyle\sum_{i=1}^{n}x_iP\left(X=x_i\right)\)
Forventningen til en kontinuerlig stokastisk variabel er:
\(E(X)=\displaystyle\int_{-\infty}^{\infty}x f(x)dx\)
hvor f(x) er sannsynlighetstetthetsfunksjonen.
Svart svane
Det finnes også et utfall hvor mynten ikke faller ned på noen av sidene, men blir stående på høykant, altså hverken mynt eller kron. Dette utfallet hører med til de ekstremt sjeldne, en svart svane. I teorien kunne man tenke seg enda et utfall, det vil si mynten faller ikke ned i det hele tatt, men forblir svevende.
Mer om myntkast (pdf)