Siden temperatur påvirker det meste av det vi kjenner til, hvem av disse forskjellige metodene å måle mengden vanndamp i luften bør man holde konstant hvis man gjør et eksperiment ved forskjellig temperatur ?
Vanndamp, en drivhusgass, har som andre gasser et trykk kalt vanndamptrykk. Clausius-Clapeyron ligningen er en differensialligning som uttrykker forandring i vanndamptrykk over en ren væske, i vårt tilfelle vann, når temperaturen endrer seg. Ligningen viser stigningen i vanndamptrykk-kurven når temperaturen øker.
\(\displaystyle \frac{de^0}{dT}=\frac{H}{R\cdot T^2}\)
hvor e0 er metningsvanndamptrykk, T er absolutt temperatur, R er gasskonstanten 8.314 mol-1 K-1 og H er latent fordampningsvarme. Ved integrering gir denne:
\(\displaystyle \ln e^0=-\frac{H}{R}\frac{1}{T}+C\)
Hvor C er en integrasjonskonstant. Imidlertid endrer latent fordampningsvarme seg med temperaturen.
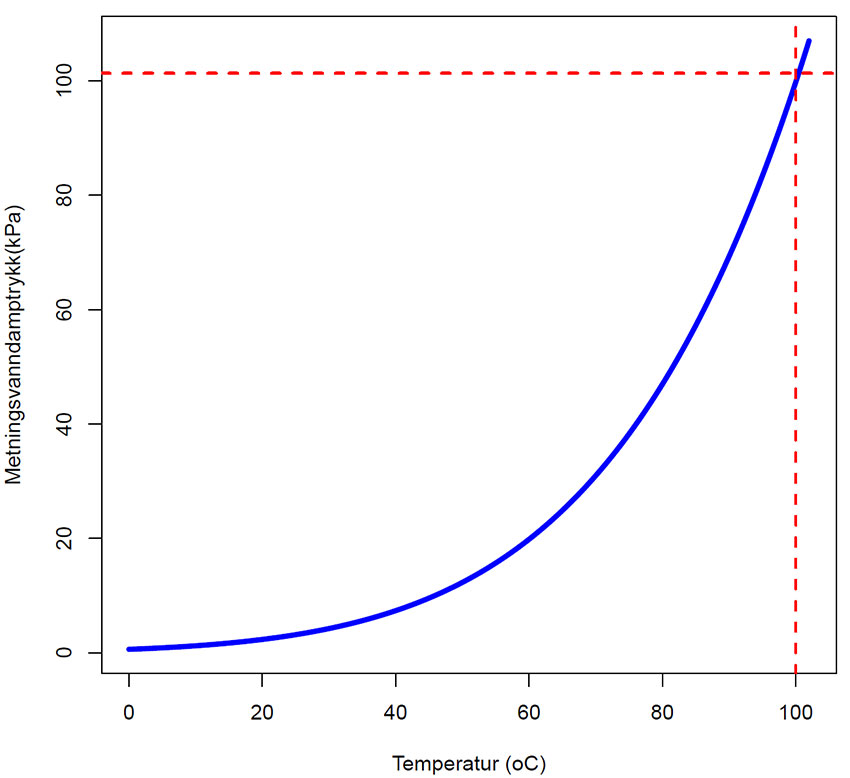
Metningsvanndamptrykk eo ved forskjellig temperatur (oC). Legg merke til at ved 100oC, når vann koker, er vanndampmetningstrykket lik lufttrykket.
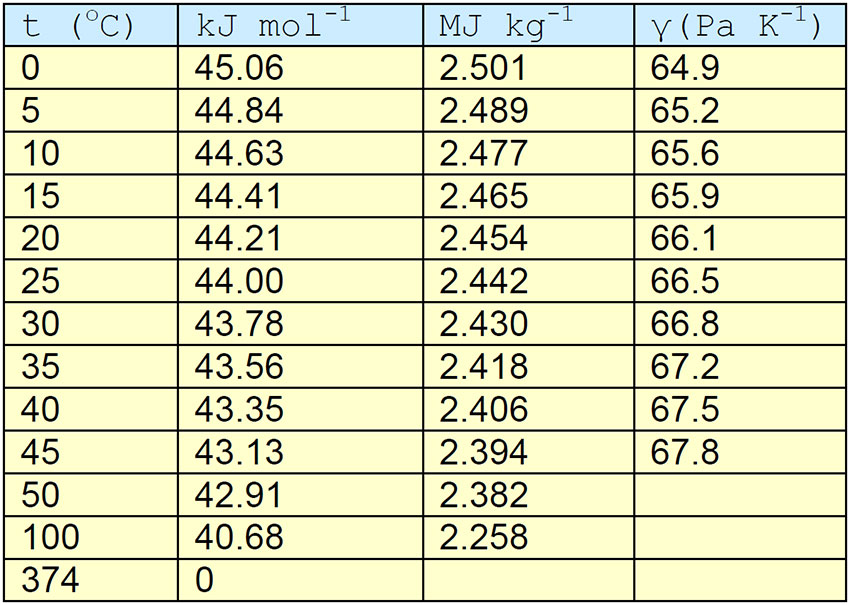
Tabell. Fordampningsvarme for vann i kJ mol-1 og MJ kg-1, samt psykrometerkonstanten γ(Pa K-1) ved forskjellige temperatur. Molekylvekt vann (H20) : 18.01528. 1kg H20=55.50844 mol

Fordampningsvarmen til vann (kJ/mpol) ved forskjellig temperatur (oC).
\(\displaystyle \frac{de^0}{dT}=\frac{H}{R\cdot T^2}\left(a+bT+cT^2\right)=\frac{e}{R}\left(\frac{a}{T^2}+\frac{b}{T}+c\right)\)
Hvor e0 er metningsvanndamptrykk, T er absolutt temperatur, R er gasskonstanten 8.314 mol-1 K-1 , e er vanndamptrykket, og H er latent fordampningsvarme som endrer seg med temperaturen ifølge den kvadratiske ligningen med polynomkonstanter a, b og c.
Denne differensialligningen kan løses ved integrering og gir:
\(\displaystyle \ln e^0=\frac{1}{R}\left(-\frac{a}{T}+b\ln T+cT\right)+C_2\)
Metningsvanndamptrykket over vann kan beregnes ut fra følgende formel:
\(\displaystyle e^0= exp\left(52.57633-\frac{6790.4985}{T}-5.02808\cdot T\right)\)
hvor exp er eksponentialfunksjonen, Hvor e0 er metningsvanndamptrykket i kPa og T er absolutt temperatur, T0=-273.16.
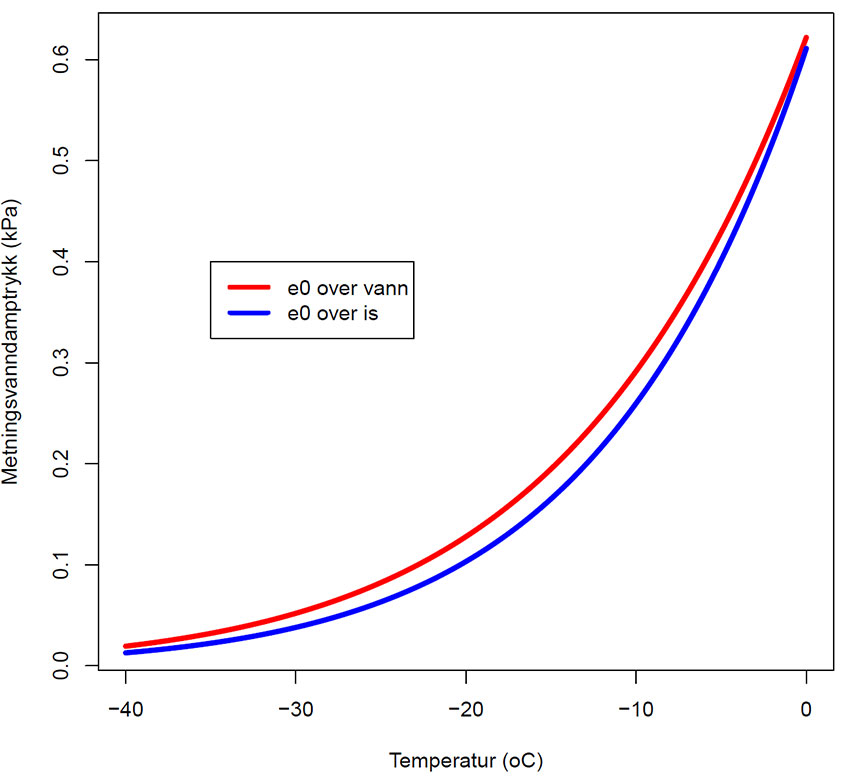
Metningsvanndamptrykk (eo) over henholdsvis is og underkjølt vann ved temperatur lavere enn 0oC. Legg merke til at vanndamptrykket over is er lavere enn tilsvarende over underkjølt vann ved samme temperatur. Dette har stor biologisk betydning ved akklimatisering til frost, hvor vann beveger seg til steder hvor det allerede er dannet is.
Det betyr at har man først fått laget is, for eksempel i intercellularrom via iskjernedannende proteiner, så vil underkjølt vann i en celle ifølge fysikkens lover bevege seg ut av cellene og ut i intercellularrommene hvor vannet fryser, og således ikke skader plantecellene. Samme fenomenet opptrer hvis man glemmer å lukke kjøleskapdøren i et kjøleskap med et eget fryserom. All fuktighet i rommet vil etter hvert samle seg i kjøleskapet.

Vanndampmetningstrykk (eo) som funksjon av temperatur oC.
Goff Gratch ligningen angir vanndamptrykket over is: (Smithsonian tables 1984):
\(\displaystyle \log e^0==-9.09718\left(\frac{T_0}{T}-1\right)-3.56654\log\left(\frac{T_0}{T}\right)+0.876793\left(1-\frac{T}{T_0}\right)+\log \left(es_0\right)\)
Hvor T0= -273.16, T er absolutt temperatur (K), es0 er metningsvanndamptrykket ved 0oC (=0.611 kPa). Metningsvanndamptrykket e0 blir uttrykt i kilopascal (kPa). Logaritmen log er med grunntall 10 (Briggske logaritmer) og vi benytter 10log y=y. Det finnes en rekke lignende formler: Arden Buck-ligningene, Hyland & Wexler, Magnus-Teten samt Murphy & Koop.
Goff Gratch ligningen som viser vanndamptrykket over underkjølt vann, vann under 0oC.
Duggpunkttemperatur er den temperaturen som luften må kjøles ned til for at det skal dannes dugg fra vanndamp som kondenserer. Ettersom den relative fuktigheten i lufta øker så blir duggpunkttemperaturen mer lik lufttemperaturen.
Hvis man kjenner relativ fuktighet (RH) og lufttemperaturen T så kan man bestemme duggpunkttemperaturen Td ut fra Magnus-Tetens tilpasningen:
\(\displaystyle t_d=\frac{bg}{a-g}\)
Hvor a=17.27 og b=237.7oC, t er temperatur i oC
\(\displaystyle g=\frac{at}{b+t}+\ln \left(\frac{RH}{100}\right)\)
Den gir en god approksimasjon fra t= 0-60oC og duggpunkt fra 0-50oC.
Vanndamptrykkdeficit (VPD)= e0 - e
Vanndamptrykker er er lik:
\(\displaystyle e=e^0-\gamma\left(t_t - t_v\right)\)
hvor tt er tørt termometertemperatur, tv er vått termometertemperatur, og gamma er lik psykrometerkonstanten.
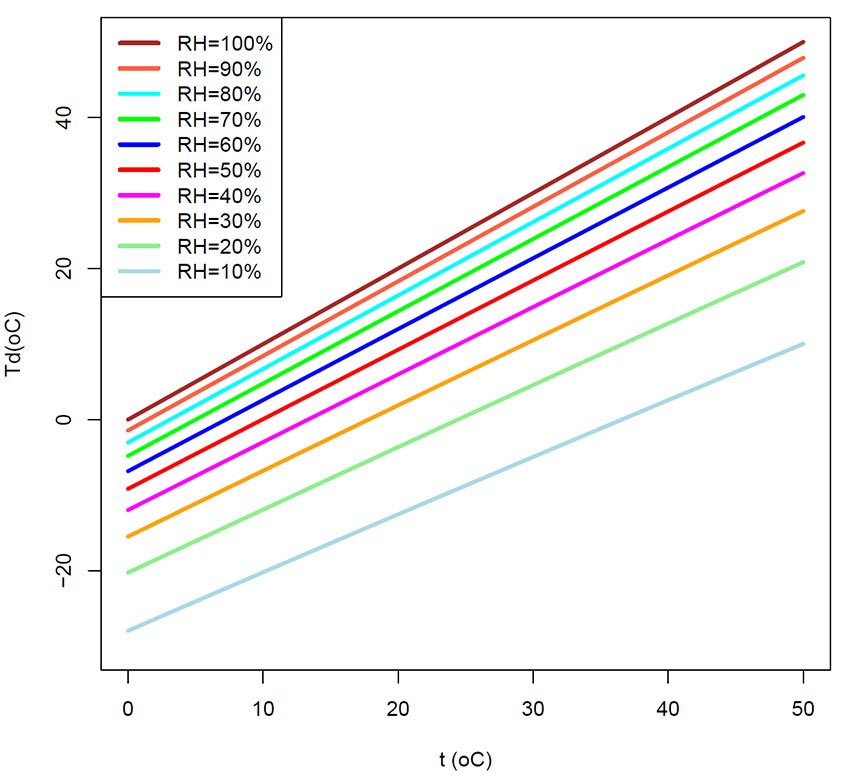
Duggpunkttemperatur Td (oC) som funksjon av temperatur t (oC) ved forskjellig relativ fuktighet (RH), med RH 10-100%
Sammenheng mellom tørt termometertemperatur (Tt, 20oC), duggpunkttemperatur (Td, 9.254oC), og vått termometertemperatur (Tv, Hvor på figuren ?) ved 50% RH. Metningsvanndamptrykk ved 20oC: 2.339901 kPa, og vanndamptrykk ved 50% RH= 1.169951. Psykrometerkonstant γ= -0.0661 kPa K-1. VPD (vanndamptrykkdeficit) er lik e0-e. RH=e/e0*100
Vi kan uttrykke vanndampinnholdet i luften som en molbrøk. Molbrøken for vanndamp i luft (wL):
\(\displaystyle w_L=\frac{e}{P}=\frac{n_w}{N}\)
hvor P er lufttrykket, e er vanndamptrykket, N er antall mol og nw er antall mol vann. Molbrøken blir derved med hhv. måleenheten Pa∙kPa-1 eller mmol∙ mol-1. Hvis vanndamptrykket er 1.27 kPa og lufttrykket er 101.3 kPa så blir molbrøken for vanndamp:
wL=1.27∙103/101.3= 12.54 Pa kPa-1.
Bruk molbrøk og ikke konsentrasjon når du regner med mengden gass i luft, da slipper du å ta hensyn til effekten av temperaturendringer.
Vannpotensialet i luft
Vi kan beregne vannpotensialet Ψ i luft ut fra formelen:
\(\displaystyle \psi=\frac{RT}{V_v}\ln \frac{RH}{100}\)
Hvor R er gasskonstanten 8,31441 J/mol•K , T er absolutt temperatur, RH er relativ fuktighet i %, Vv er molvolumet for vann. Ψ er vannpotensialet i MPa, og ved 20oC (293K) er
RT/Vv =135MPa
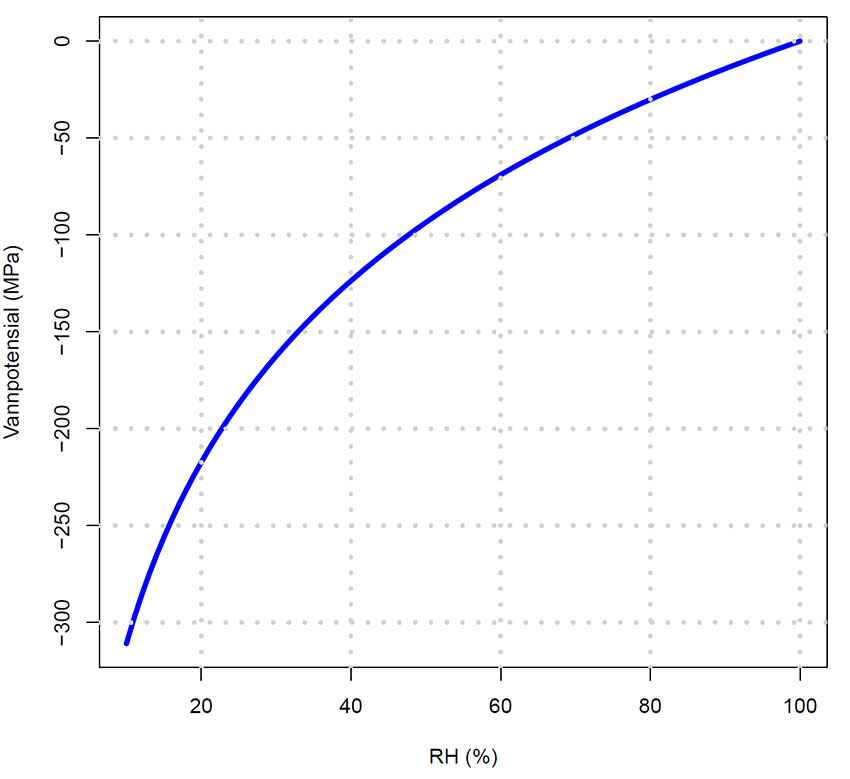
Vannpotensial Ψ (MPa) som funksjon av relativ fuktighet (RH) i lufta. Det er det lave vannpotensialet i luft ikke mettet med vanndamp som lager tensjonen i vannfilmen i celleveggene i bladet, og som gir drivkraften for vanntransporten i vedvevet (xylem). Når lufta er mettet med vanndamp (RH=100%) er vannpotensialet lik 0, og hos urtaktige planter kan man i dette tilfellet registrere rottrykk.
Lufttrykk og hoh
Lufttrykket p varierer med høyden over havet:
\(\displaystyle p=101.86425\cdot e^{-1.24087 \cdot 10^{-4}h}\;\; 0-1524\;moh\)
\(\displaystyle p=102.12563\cdot e^{-1.25184 \cdot 10^{-4}h}\;\; 1525-3048\;moh\)
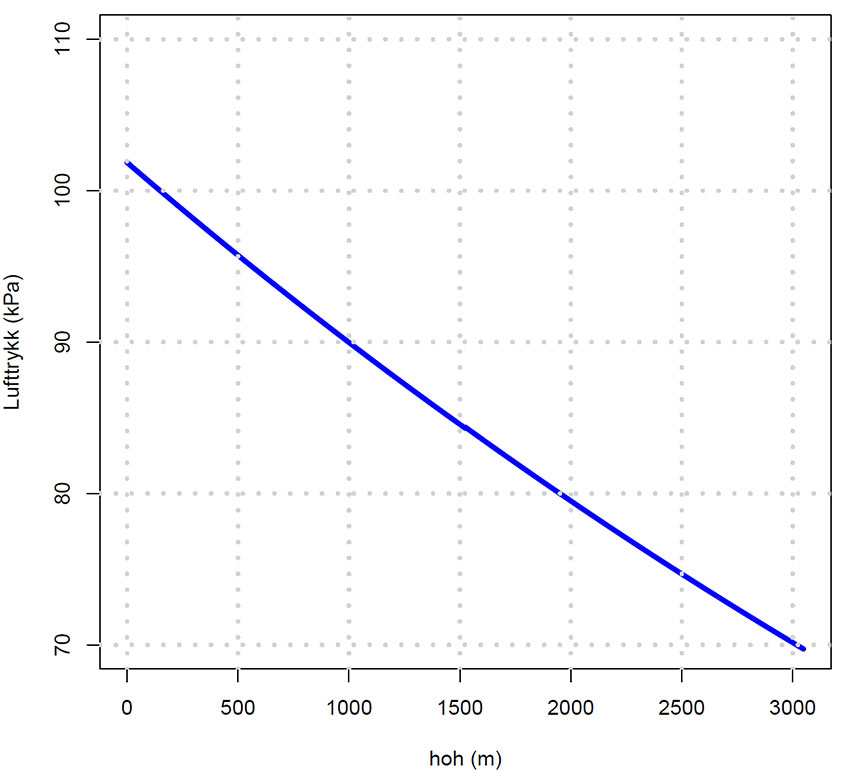
Lufttrykk (kPa) som funksjon av høyden over havet , hoh (m).
Standard atmosfæretrykk (STP) er 101325 Pa = 101-325 kPa = 1.013 bar = 760 millimeter kvikksølv (Hg).
Innhold av gasser i lufta i troposfæren:
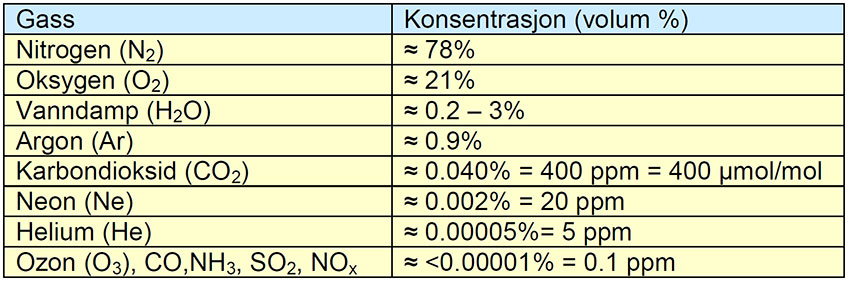
Trykket (P) til en gass er avhengig av volum (V), temperatur (T) og antall mol av gassen (n), R er gasskonstanten. Vanndampinnholdet i lufta varierer, og siden totaltrykket varierer med partialtrykkene så vil partialtrykket til vanndamp påvirke totaltrykket (Daltons lov), og skape trykkforskjeller. Dette prinsippet blir anvendt i luftsirkulasjon i rotstokken hos vannliljer og andre sumpplanter.
Gasslovene
Boyle-Mariottes lov: Trykk (P) ganger volum (V) er konstant
\(\displaystyle VP=\;konstant\)
Gay-Lussacs lov: Volumet (V) for en bestemt gassmengde ved konstant trykk er proporsjonal med temperaturen (T):
\(\displaystyle\frac{V}{T}=\;konstant\)
Ved å sette disse to lovene sammen får vi den generelle gassloven:
\(\displaystyle\frac{PV}{T}=\;konstant\)
Avogadros lov: Like volumer gass under like ytre betingelser innholder samme antall molekyler. 1 mol inneholder Avogadros tall partikler: 6.022∙1023 partikler. Molvolumet ved 0oC og 0.1013 MPa er 22.414 liter. Molvolumet ved en annen temperatur bestemmes vha. Gay-Lussacs. Ved å bringe inn Avogadros lov får den generelle gassloven formen:
\(\displaystyle PV=nRT\)
Daltons lov om partialtrykk sier at i en gassbladning hvor gassene ikke reagerer med hverandre er partialtrykket til hver gass lik trykket som den utøver alene, og totaltrykket (P) er summen av partialtrykkene (pn):
\(\displaystyle p=p_1 +p_2+p_3+...+p_n\)
Regneeksempel
Vi har en plantevegetasjon under følgende betingelser. Lufttemperaturen omkring vegetasjonen er 20 oC, relativ fuktighet er 67 %, temperaturen til bladet er 21 oC, lufttrykket er 99 kPa, vannpotensialet i bladet er -1 MPa, Inne i vegetasjonen er tørt termometertemperatur 19 oC og fuktig termometertemperatur 14 oC.
Beregn følgende:
a. vanndamptrykket i lufta e
\(\displaystyle e=\frac{2337\; Pa \cdot 67}{100}=1565\; Pa\)
b. metningsvanndamptrykket i lufta eo
eo =2337 Pa (tabell)
c. vanndamptrykkdeficit VPD i lufta
VPD = 2337 - 1565 = 772 Pa
d. vanndamptrykkdeficit i bladet
VPDblad = 2486 - 1565 = 921 Pa
e. forskjellen i vanndampmolbrøk mellom vegetasjon og lufta omkring
\(\displaystyle \Delta w =\frac{2486-1565}{99}=9.3\; Pa\; kPa^{-1}\)
f. vannpotensialforskjellen mellom blad og luft
\(\displaystyle \Psi_ {luft}=1.06T\log \frac{RH}{100}=1.06 \cdot 293 \cdot\log \frac{67}{100}=-54.02 \;MPa\)
g. duggpunktet i lufta omkring vegetasjonen
Temperaturen når 1565 Pa er vanndamptrykket er 13.7 oC som er duggpunktet i lufta.
Forskjellen i vannpotensial ΔΨ= 53 MPa, siden bladet hadde vannpotensial -1 MPa
h. duggpunktet i vegetasjonen
\(\displaystyle e=e_o -\gamma \left(T_t - T_f\right)=1598-65.9\;\left(292-287\right)=1268\; Pa\)
Når 1268 Pa er metningsvanndamptrykket er duggpunktet 10.5 oC i vegetasjonen.
Varmeledning er massefri transport av varme over en strekning. Har liten betydning i planteriket. Jfr. en teskje av sølv og en teskje av tre i varmt vann.
Varmelagring. Henger sammen med massen og spesifikk varmekapasitet i lagringsmediet. Man kan f.eks. anta at det er tilnærmet likt for vann eks. 4.19 kJ kg-1 K-1 ved 20 oC.
Hvis fotosyntesen er 1 μmol m-1 s-1 tilsvarer dette i energi (W m-2)
\(\displaystyle Q_{FS}=1\cdot 10^{-6}\; mol \; m^{-2}\; s^{-1}\cdot 477 \cdot 10^3 \; J\; mol^{-1}=0.477\; W\; m^{-2}\)
Varmetap Q ved transpirasjon:
\(\displaystyle Q_{transpirasjon}= J_{H_2O}\Delta H_{fordampning}\)
F. eks. hvis vanndampfluksen JH2O= 1 mmol m-2 s-2 så blir :
Qtranspirasjon = 1 mmol m-2 s-1 · 44 kJ mol-1 = 44 W m-2
Litteratur
Etherington JR: Environment and plant ecology. W.H. Freeman & Comp. 1983
Lambers H, Chapin III FS & Pons TL: Plant Physiological Ecology. Springer Verlag 1998.
Larcher W : Physiological plant ecology, Springer Verlag 1995.
Nobel PS: Physicochemical and environmental plant physiology. Academic Press 1991.
Monteith JL. & Unsworth MH: Principles of environmental physics. Edward Arnold 1990.
Willert, D.J.v, Matyssek, R. & Herppich, W.: Experimentelle Pflanzenökologie. Georg Thieme Verlag 1995.
Teksten er hentet fra Vanndamp og vanndamptrykk