Modeller er viktige i all vitenskap. Man kan lage en matematisk modell av et økosystem, en populasjon eller av været brukt i meteorologenes klimamodeller. I arbeidet med modellen samles og systematiseres kunnskap. Modellen brukes til å forstå systemet, forutsi hendelser og trekke konklusjoner fra modellen, og se om det modellen predikterer stemmer med virkeligheten. Modellen har et sett med tilstandsvariable som oppsummerer egenskapene til systemet. Dynamiske ligninger viser hvordan tilstandsvariable endrer seg over tid. Måleenhetene på venstre side av likhetstegnet i differensialligningene må være lik måleenhetene på høyre side.
Den tiden man kjente til bare 6 planeter trodde man at avstanden mellom dem var bestemt av 5 lineære polyedre , Platonske legemer: tetraeder (4 trekantede sideflater), heksader (kube, 6 kvadratiske sideflater), oktader( 8 trekantede sideflater), dodekader (12 femkantede sideflater) og ikosader (20 trekantede sideflater).
Johannes Kepler (1571-1930) kunne beskrive planetenes bevegelser i form av 3 lover som ga forklaring på Tycho Brahes observasjoner.

1. Planetbanene er elipser med Sola i brennpunktet. 2. Planetene sveiper like store arealer på lik tid. 3. Tredjepotens av planetenes avstand fra sola er proporsjonal med kvadratet til siderisk omløpstid.

På siste del av 1600-tallet studerte Newton av bevegelsen av Sola og Jorden, et tolegemesystem i klassisk mekanikk karakterisert av bevegelse, posisjon og hastighet som funksjon av tiden, og som kunne beskrives med differensialligninger. Isaac Newton la et grunnlag for differensial- og integralregning mer verket Philosophiae naturalis principa mathematica (Det matematiske prinsipp for naturfilosofi) publisert i 1687. En fallende ball kan beskrives av to variable, høyde (h) og hastighet (v) og begge er funksjoner av tiden (h(t), v(t)). Lager vi en grafisk framstilling av posisjon som funksjon av tid gir denne kurven informasjon om hastighet, stigningen av grafen er et mål på hastigheten. Hastighet er endring i posisjon, og endring i hastighet er aksellerasjon (a). Endringen kalles den deriverte.
Bevegelsesmoment= masse(m)∙hastighet.
Ifølge Newtons andre lov er kraft (F)= masse ∙aksellerasjon.
\(\displaystyle F=ma\)
Newton fant at ved havnivå er gravitasjonskraften lik m∙g, hvor g=9.8 ms-2 ved havoverflaten.
Ifølge Leibniz er endring i høyde som funksjon av tid lik hastighet, og endring i bevegelsesmoment er lik gravitasjonskraften, med negativt fortegn fordi gravitasjonskraften virker nedover.
\(\displaystyle \frac{dh}{dt}= v\;\;\;\;\;\; \frac{dmv}{dt}=-mg\;\;\;\;\;\; \frac{dv}{dt}=a\)
Kastes en ball rett opp minker hastigheten inntil ballen når sitt høyeste punkt hvor hastigheten er 0, v=dh/dt=0, deretter begynner ballen å falle nedover og hastigheten øker, men aksellerasjonen er hele tiden konstant, -g. Det ble William Rowan Hamilton (1805-1865) som fikk sitt navn knyttet til Hamiltonsk mekanikk, bevegelsesligninger i symmetrisk form, en viderutvikling av Lagranges mekanikk.
Differensialligningene i Newtons mekanikk for en fallende ball kan brukes til å beskrive bevegelsen av planeter. Den matematiske verden gir forståelse av den fysiske verden.
Ifølge Newtons inverse kvadratlov for gravitasjonstiltrekning vil to objekter med masse m1 og m2 tiltrekke hverandre med en kraft som er proporsjonal med massene og inverst proporsjonalt med kvadratet av avstanden (r) mellom dem.
\(\displaystyle F=\frac{G m_1m_2}{r^2}\)
G er gravitasjonskonstanten G=6.67∙10-11 N m2 kg-2, og gravitasjonen virker i en retning langs en linje som forbinder sentrene i de to massene,
Dette gjelder for alle to-objekt systemer, en planet rundt sola, eller en måne rundt jorda.
Det viste seg at trelegemesystemet med jord, måne og sol var vanskelig å løse. Vi kan imidlertid summere alle krefter som virker på et objekt. Hva er gravitasjon og hvor kommer gravitasjonskreftene fra ? Kunnskapen om gravitasjon gjorde at noen ble bekymret. Vil alle planeter fortsette å følge omtrent samme bane, eller kan en planet skli ut av sin bane og nærme seg solen, eller bevege seg ut i verdensrommets mørke ? Kong Oskar II utlovet en pris på 2500 kroner til den som kunne løse n-legemeproblemet. Det vil si å finne differensialligningene som beskriver planetbevegelsene i all framtid, gitt posisjon og hastighet. Newton hadde funnet svaret for n=2.
Er n-legeme problemet uløselig ? Hver planet påvirkes av alle andre planeter, sola, måner, asteroider, kometer osv.
Den franske matematikeren Jules Henri Poincaré (1854-1912) fikk prisen på kongens 60-årsdag 21.1.1889, men han hadde egentlig ikke løst problemet.

Dette var pinlig for den svenske matematikeren Gösta Mittag-Leffler (1846-1927), samt Karl T. Weierstrass, professor i Berlin, og Cherles Hermite som satt i juryen. Prispengene ble tilbakelevert, men i 1890 publiserte Poincaré den riktige løsningen: Sur le probléme des trois corps et et les equations de la dynamique i Acta Matematica 13 (1890)1-270.
I tre-legemeproblemet sol-måne-jord hadde Poincaré for hvert av objektene tredimensjonalt 3 koordinater for hastighet og 3 koordinater for posisjon, i alt 18 variable for sol-måne-jord, som kan betraktes som et punkt som beveger seg i et 18-dimensjonalt rom. Det nye var at Poincaré valgte en geometrisk tilnærming for løsning av differensialligninger uten å spørre etter kvalitative egenskaper, en geometrisk analyse av stabilitet.
Fra dynamikk til geometri
Løsningene av differensialligningene kan presenteres geometrisk som trajektorier i et faserom. Trajektoriene kan gå i løkker, periodiske baner, men trajektoriene kan ikke krysse hverandre fordi det er umulig å trekke mer en en tangent gjennom et punkt. Kurver gjennom det globale faseportrett kalles løsningskurver, baner eller trajektorier. Differensialligninger er det samme som geometriske bilder av flyt. Å løse differensialligninger er å finne den generelle løsningen som er lik flyt. Man må sikre seg at det finnes løsninger, dvs. variabelen kan presenteres som funksjon av tid. Trajektoriene starter i et punkt i faserommet og man må løse initialverdiproblemet. Det er vanskelige å finne formelen for alle tilstandsvariablene, hastighet og posisjon i ethvert tidspunkt, gitt initialverdier for hastighet og posisjon. Global eksistens vil si kurver definert for hvert punkt i fortid, nåtid og framtid. Lokal eksistens vi si bare i et kort tidsintervall: før, nå, etter. Kontinuerlig løsning m.h.p initialdata gjør at trajektoriene ligger nær hverandre i starten.
Bifurkasjoner er endringer i et dynamisk system når en eller flere parametere passerer kritiske verdier. Noen systemer viser hysterse, hvor bifurkasjoner får forskjellige verdier avhengig av retningen på endringen av parameterverdiene. Poincaré betraktes som grunnlegger av teorien om bifurkasjoner.
To trajektorier som ligger nær hverandre atskilles raskt og eksponensielt og kan beskrives via Lyapunoveksponenten λ. Russisk matematiker Aleksandr Mikhailovich Lyapunov (1857-1918).

Sofya Kovalevskaya (1850-1891) ansatt som professor ved Universitetet i Stockholm kom tidligere med tilsvarende idéer.

Lyapunoveksponenten er alltid et reelt tall og gir et mål på hvordan to trajektorier atskilles. Positiv eksponent angir kaos, negativ eksponent angir en periodisk syklus eller et fast punkt. Det er likhetstrekk med egenverdier og begge kan beregnes ut fra Jacobi-matriser, og begge angis med bokstaven lambda. Liapunoveksponenten gir et kvantitativt mål på vekst eller reduksjon i løsningen til lineariserte ligninger i forskjellige retninger i faserommet. For et n-dimensjonalt rom er det n Lyapunoveksponenter hvor λ er størst, og λ avhenger av hvilke trajektorier man studerer. Hvis vi plotter den naturlige logaritmen ln til vektoren som funksjon av tiden som mål på atskillelsen av trajektoriene blir dette en tilnærmet rett linje med topper og daler, og som etter hvert når metning. Stigningen av denne linjen er gitt ved λ. Man kan bare prediktere fremtiden bare noen få multipler av 1/λ, hvilket betyr at det er vanskelig å prediktere oppførselen av kaotiske systemer jfr. værmeldinger. Kaotisk, betyr ikke uten orden, men kaotiske systemer er meget følsomme for initialbetingelsene. Framtiden utover et lite kort tidsrom er totalt uforutsigbar.
Poincaré avbildninger (Poincaré snitt)lager et kutt i alle trajektoriene, dvs. kutter alle flytlinjene i et dynamisk system og viser hvordan dette blir seende ut i et plan. Man kan tenke seg en tyggegummi som kan strekkes i alle retninger, og Poincaré-avbildningen projiserer faste punkter på tyggegummien ned i ett plan. Avbildningen gir punkter på en flate med to koordinater og viser hvordan koordinatene endrer seg når trajektoriet går tilbake til flaten. Periodiske løkker har trajektorier som flyter rundt og treffer seg selv (Jfr. Lotka-Volterra), og Poincaré-avbildningen blir i dette tilfellet ett punkt. Finner man faste punkter i en topologisk Poincaré transformasjon betyr dette at det må være periodiske sviningninger i det dynamiske systemet.
Kaos er avhengig av initialbetingelsene og svært følsomme for disse. Feigenbaum sammenlignet kaos og fasetransisjoner. May viste at det for høye veksthastigheter oppstår kaos i den logistiske ligning.
Kaotiske systemer er aperiodiske og er svært følsomme for initialbetingelsene. Systemet kan beskrives av ikke-lineære ligninger, og små endringer i en parameter er avgjørende om systemet oppfører seg kaotisk. Kaos kan vises i et Poincaré-snitt. I 1963 kunne Lorenz vise at tre differensialligninger som beskrev værfenomener oscillerte irregulært og nådde ikke likevekt, Lorenz sommfugleffekt: Et vingeslag i Brasil kan gi en tornado i Texas.
På 1970-tallet kunne biologen Robert May vise at det oppstod kaos i den logistiske vekstligningen ved høye veksthastigheter. Kaos (gr.) betyr fravær av orden, og kaos er aperiodisk oppførsel følsom for initialbetingelsene. Meget små forandringer i utgangsbetingelsene gir meget forskjellig resultat, selv i samme ligning. Væske og luft består av store mengder molekyler som kan strømme laminært eller turbulent, og turbulent strøm gir kaos (kaotisk turbulens. For eksempel omrøring av tykk fløte i en kaffekopp. Mens planetene går i stabile elipsebaner rundt sola, går den lille månen Hyperion i en kaotisk bane rundt Saturn.
Belousov-Zhabotinsky ringer er eksempler på kaotiske kjemiske oscillasjoner (spiralbølger) ved oksidasjon av malonsyre i en sur løsning med bromationer med små mengder metallioner, cesium eller jern som katalysator. Kaotisk leketøy er satt sammen av to pendler som svinger.
Mandelbrot var en av pionerene innen fraktalgeometri, et resultat av interasjonsprosesser i enkle ligninger. Feigenbaum studerte av faseoverganger og kaos. Datamaskiner gjorde det mulig å visualisere deterministisk kaos fra ikke-lineære ligninger og synliggjort strukturer og mønstre som gjentar seg.
Det er svært vanskelig å forutsi utviklingen av komplekse systemer. På noen stadier kan de begynne å oppføre seg kaotiske og uforutsigbare, men det som skjer er allikevel ikke tilfeldig. På visse steder svinger systemet mellom to rytmer, og det skjer en todeling (bifurkasjon). Deretter kan det skje helt uregelmessige og uforutsigbare reaksjoner uten noen fast rytme dvs. systemet oppfører seg kaotisk. For økologene har kaosmodellene og fraktale mønstere vært med på å forklare utviklingen av populasjoner og hvordan formen på en plante oppstår. Ofte kan populasjoner svinge uten å nå en likevektssituasjon og variasjonen synes å være usystematisk. Det fantes tidligere ingen fullgod matematisk beskrivelse av denne situasjonen. Det er så mange faktorer ute i naturen som påvirker et system at det er vanskelig å finne noe mønster i virvaret, men det er en struktur. Det kan plutselig finnes "vinduer" i kaoset hvor populasjonen faller til ro omkring en likevektsverdi. Seinere går det på nytt inn i kaos. Forgreiningene i fikentreet oppstår med stadig kortere mellomrom, og intervallene mellom periodefordoblingen minsker med faktoren 4.669201.., kalt Feigenbaums tall. Det er også en gjentakelse av mønsteret for periodefordoblinger og overgang til kaos. Man sier at systemet viser selvsimilaritet. Det er i den kaotiske delen mønsterstrukturer gjentar seg i miniatyr om og om igjen. Benoit Mandelbrot har vist dette via Mandelbrot-mengden: Han gjentok en enkel beregning en rekke ganger og resultatet av denne danner utgangspunktet for den neste (iterasjoner). Det er altså en uendelighet i dette mønsteret og man kan zoome inn på stadig mindre deler av helheten. Lengden av kysten er avhengig av målestokken man bruker. En mikrostruktur går igjen. Helhetens form er identisk med delenes form. Hvis en rett linje har dimensjon en, flaten har dimensjon to og rommet dimensjon tre, vil krøllete linjer har en dimensjon som ligger mellom disse heltallene, kalt fraktaler. Kaosforskningen er istand til å gi mønstre og lovmessighet bak dynamiske systemers utvikling. Mønstre oppstår når delene i et system plasserer seg energimessig mest gunstig i forhold til hverandre for eksempel vannmolekyler i en snøkrystall.
Differensialligninger har en kontinuerlig tidsakse, mens differensligninger har diskrete tidsintervall.
En viktig del av topologi er studiet av posisjon. Topologisk sett er det ingen forskjell på en sirkel, elipse eller en annen lukket kurve. En todimensjonal manifold er et objekt hvor et punkt og de nærmeste omgivelser kan betraktes som en flate. For en matematiker er kulen todimensjonal, ser bort fra det som er inne i kulen. Leve på en kule er å leve på en flate. En smultring, torus, er også en todimensjonal manifold. Det er først når vi kommer utenfor jordkloden at vi kan se at vi lever på en kule. Ser man seg rundt ser det ut som man lever på en flate. En tredimensjonal manifold må være tredimensjonal på et ethvertpunkt på objektet.
I det følgende skal vi først se på systemer med en variabel: et lineært system i form av eksponensiell vekst eller nedbrytning, og det ikke-lineære systemet med logistisk vekst som under visse betingelser viser bifurkasjoner og kaos. Newtons system med sol og måne var et lineært system med to variable, men vi skal se på det ikke-lineære systemet Lotka-Volterra-modellen for predator-byttedyr. Det lineære Poincarés trelegemeproblemet har tre variable, og vi skal studere de ikke-lineær Lorenzligningene, og samt se litt på fraktaler, diffusjon, rute-systemer og cellulære automater e.g. Conways "game of life" ("livets spill"). Schrödingers bølgligninger innen kvantemekanikk, Maxwells ligninger for elektromagnetisme, Ficks diffusjonsligninger, Fouriers varmeligninger, Laplaces ligning for harmoniske funksjoner, Navier-Stokes ligningene (flyt av væske eller gass i rør hvor hastigheten er størst i midten og minst ved veggen med tilhørende turbulens), samt Black-Scholes ligninger for beregning av pris på aksjeopsjoner i finansverden, er alle eksempler på differensialligninger.
Kolmogorov-Arnold-Moser teori.
Biologiske systemer er selvorganiserende dissipative energiforbrukende systemer langt fra likevekt. Det er flukser av stoff og energi gjennom de biologiske systemene, beskrevet av irreversibel termodynamikk av bl.a. Prigogine og norskamerikaneren og nobelprisvinneren Lars Onsager.
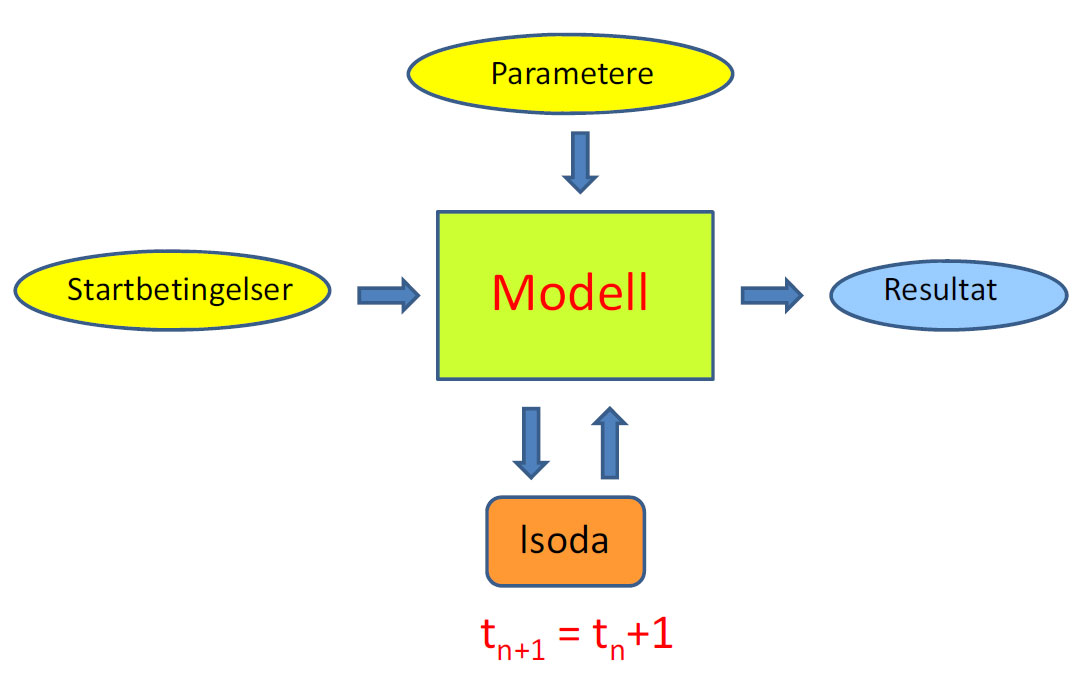
Gitt et modellsystem beskrevet av differensialligninger. Ved gitte startbetingelser, parameterverdier og et bestemt antall tidstrinn t så vil differensialligningene kunne løses numerisk via en odesolver, her lsoda fra R.
Naturforskeren studerer ikke naturen fordi det er nyttig. Han/hun studerer den fordi han fryder seg, og han fryder seg fordi det er vakkert. Hvis naturen ikke var vakker, så ville det ikke være verdt å vite, og hvis naturen ikke var verd å vite, så ville ikke livet være verd å leve. J.H.Poincaré.