Ifølge gresk mytologi og Hesiods i Theogoni (Gudenes skapelse) var verden et opprinnelig et tomt mørkt uordnet rom khaos. Fra Khaos oppstod jordgudinnen Gaia, nattgudinnen Nyx , underverden Tartaros og kjærighetsgudinnen Eros. Det er mange skapelsesmyter fra khaos.
Selv om man har deterministiske ligninger så vil kaos, også kalt deterministisk kaos, gjøre det vanskelig å prediktere (forutsi) hvordan et system vil oppføre seg over tid. Deterministisk vil se at det er ingen tilfeldighet i utviklingen av systemet, det kan predikteres. Systemer som i utgangspunktet er deterministiske kan opptre uforutsigbart og gi deterministisk kaos. Pseudorandome (pseudotilfeldige) slumptallsgeneratorer er deterministiske, men vanskeig å prediktere. Markov-kjeder og ”random walk” (Brownske bevegelser) er eksempler på ikke-deterministiske prosesser.
Den logistiske vekstligningen betraktet i tidstrinn som en differensligning gir kaos ved store veksthastigheter, i motsetning til den logistiske vekstligningen som differensialligning. Bifurkasjoner kan gi kaos og turbulens. Kaotisk oppførsel finner man bl.a. innen vær, klima, finans og økonomi, oscillerende kjemiske reaksjoner (Brusselator, Belousov-Zhabotinsky med bromat, malonsyre, svovelsyre og ferroin), samt populasjonsbiologi og dynamikk (datasett:Nicholsons ullspyflue, gaupe-snøskohare). Kaotiske systemer er bare predikterbare en viss tid, så blir de tilfeldige. Alt endrer seg med tiden.
Tidsskalaen for usikkerhet, Lyapunov-tiden, er bare noen få dager for den sannsynlige framtidsbeskrivelse av vær, men for utviklingen av solsystemet kan Lyapunov-tiden være millioner av år. Lyapunov-eksponenten \( \lambda \)gir et mål på hvor raskt to trajektorier atskilles seg fra hverandre \( |\delta Z(t)|\), gitt to punkter i faserommet med meget kort avstand fra hverandre \( |\delta Z_0(t)|\).
\(\displaystyle \mid \delta Z \left ( t \right ) \mid \approx e^ {\lambda t}\mid \delta Z _0 \left ( t \right ) \mid\)
Kaos og Lorenz-ligningene
Meteorologen Edvard N. Lorenz ved MIT viste i 1963 hvordan konveksjonsstrømmer i atmosfæren kunne bli beskrevet av tolv differensialligninger, som han forenklet til tre ligninger, hvor x er hastighet på rotasjonen (styrken på konveksjonsbevegelsen), positiv med klokka, negativ mot klokka; y er temperaturforskjell mellom stigende og synkende strøm, z er avvik fra linearitet i den vertikale temperaturprofilen, r er Rayleightall (dimensjonsløst) for oppdrift av luftbevegelsene, s er Prandtl tall som beskriver egenskapene til luftstrømmen, b helnings ratio i en konveksjonssylinder. Startverdiene (initialverdiene) var s =10, b=8/3 og r=28.
(Deterministic nonperiodic flow J. Atmos.Sci. 1963, 20, 130).
\(\displaystyle {dx \over dt} = s \left ( y - x \right )\)
\(\displaystyle {dy \over dt} = -xz + rx -y\)
\(\displaystyle {dz \over dt} = xy - bz\)
Løsningene oscillerer, men inne visse grenser, i form av en fraktal med dimensjon to til tre. Ligningene inneholder to kvadratledd xy og xz. Hvis løsningene x(t) blir plottet mot z(t) gir dette en figur som ligner på en sommerfugl.

Figuren viser grafisk løsningen av differensialligningene med et fasediagram x versus z for Lorenz attraktor, med konstanter r = 28, s = 10 og b = 8/3, inititalverdier (1, 1, 1) og tid 0 til 100 i trinn 0.01. Det ser ut som linjene krysser hverandre i et todimensjonalt-plot, men i et tredimensjonalt plot ville vi ha sett at dette ikke stemmer. Det er bare en unik løsning i hvert punkt. Det er mulig å trekke bare en tangent i et punkt på løsningskurven. Initialverdiene som et blått punkt. Ligningene er løst med ode-solveren lsoda i pakken deSolve i R.
I et punkt på en linje kan det bare trekkes en tangent. Trajektoriet starter nær 0, svinger til høyre og inn i sentrum av en spiral på venstre side. Trajektoriet forlater spiralen etter å ha kommet en kritisk verdi vekk fra sentrum, og etter å ha gått i spiral spretter den over til høyre side, går litt i spiral, så over til venstre side, går litt i spiral osv. Det blir seende ut som to sommerfuglvinger. Dette skyldes oppadgående og nedadgående luftstrømmer. Lorenz viste at det å kommer med en sikker værmelding langt fram i tid er vanskelig, for ikke å si umulig. Framtiden er uforutsigbar. Resultatet er avhengig av utgangsbetingelsene, men selv om startbetingelsene er målt nøyaktig vil det alltid bli en feil mellom estimert verdi og sann verdi. Det er bare en viss tid fremover det er mulig å prediktere, det vil si komme med en statistisk sannsynlighet for en utviklingsretning. Det er dette som gjenspeiles i den berømte: Does a flap of a butterfly´s wings in Brazil set off a tornado in Texas (1972).
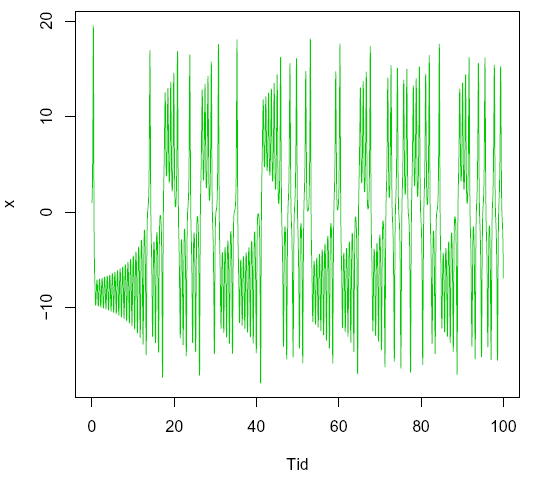
Figuren viser et tidsserieplot av x-koordinaten. Etter en periode med stabile løsninger for x starter etter en viss tid systemet å oppføre seg kaotisk med irregulære oscillasjoner og uforutsigbart. Hvis man lager at plot av maksimalverdier mn mot neste maksimalverdi mn+1osv. så får man en Lorenz avbildning.
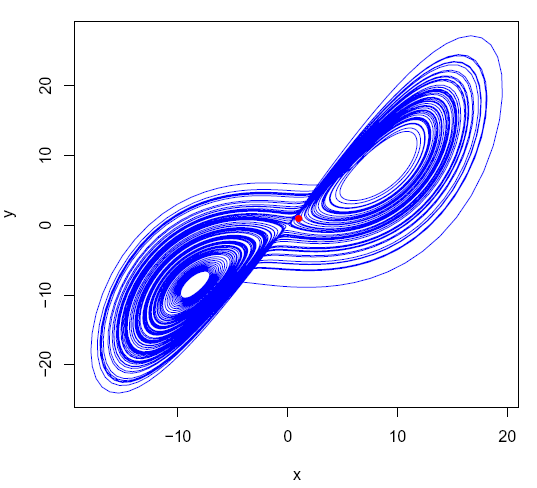
Figuren viser grafisk løsningskurvene for x versus y for Lorenz attraktor, med betingelser som vist foran.

Figuren viser grafisk løsningskurvene for y versus z for Lorenz attraktor, med betingelser som vist foran.
Trelegemeproblemet og geometrisk visualisering av løsningskurver
Keplers empirske oppdagelse og Newtons teoretiske i Principia (1687) viste hvordan gravitasjonskreftene påvirket to objekter, men det var den franske matematikeren Jules Henri Poincaré (1851-1912) som fant en løsning på trelegemeproblemet Jorden-Sola-Månen, et system med 18 dimensjoner som omfatter posisjon, hastighet og masse. Dette systemet har ingen analytiske løsninger, men løsningskurvene (integralkurvene) for differensielligningene kan visualiseres geometrisk. Poincaré oppdaget at det kunne være kaos i et determistisk system. I generell form n-legemeproblemet. Den svenske matematikeren og professor Gösta Mittag-Leffler ved Stockholms högskole og grunnlegger av tidsskriftet Acta Matematica (1882) tok initiativ til en internasjonal matematikkonkurranse, til ære for kong Oskar II på hans 60-årsdag, og med en gullmedalje og prispenger 2500 svenske kroner til den som klarte å løse 3-legemeproblemet. Juryen bestod av Mittag-Leffler, Charles Hermite og Karl Weierstrass. Poincaré kom med forslag til løsning: Sur le problème des trois corps et les équations de la dynamique (1889), og ble kåret til vinner, men oppdaget selv at han hadde regnet feil. Det hele ble meget pinelig, men endte med at Poincaré kom med en revidert versjon i 1890 som inneholdt mulighet for kaotisk bevegelse og ustabile periodiske løsningskurver (trajektorier) i faserommet. Seinere skrev Poincaré trebindsverket Les méthodes nouvelles de la mécanique céleste, og introduserte begrepet homokline baner og kaotisk oppførsel. Kolmogorov–Arnold–Moser-teori for komplekse systemer og nettverk-teoremet om kvasiperiodiske bevegelser påvirket av små forstyrrelser. Navn etter Andrey Kolmogorov (1903 – 1987), Vladimir Arnold (1937 – 2010) og Jürgen Moser (1928 – 1999), og omhandler også 3-legemeproblet først studert av Poincaré som er kaotisk med øyer at stabilitet.
Arenstorf-bane
Samme problem hadde man i forbindelse med amerikanerenes månelandinger i Apollo-programmet, objektene Jorden- Månen-Månerakett/månelandingsfartøy. Et spesialtilfelle av 3-legemeproblemet hvor det ene objektet, en satellitt har masse tilnærmet lik null. Den amerikanske matematikeren Richard F Arenstorf fant en stabil bane formet som et 8-tall med Jorden og Månen i hver sin løkke, Arenstorf trelegemeproblem . Arenstorf bidro også til å finne redningsveien for Apollo 13. Jfr. spillefilmen Apollo 13 med Tom Hanks.. (Arenstorf, RF (1963) Periodic solutions of the restricted three-body problem representing analytic continuations of Keplerian elliptic motion. Am. J. Math. 85:27-35).
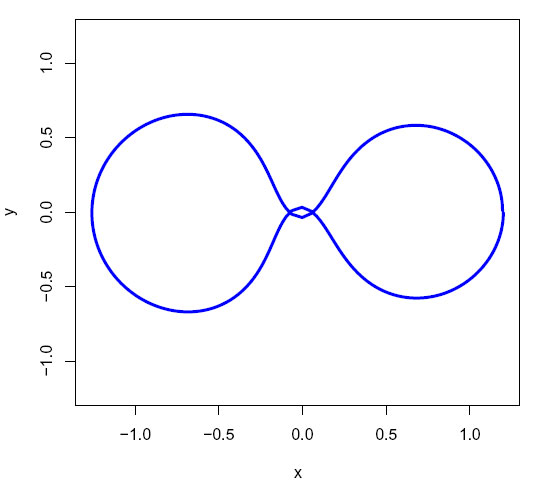
Arentorf-bane hvor henholdsvis Jorden og Månen befinner seg inne i hver sin halvdel av 8-tallet
Fraktaler
Fraktaler (l. fractus – brudd) er et gjentatt geometrisk mønster, selvsimilaritet, et mønster som gjentas og gjentas i forskjellige skalasystemer. Benoit Mandelbrot formulerte i 1967 problemstillingen: How long is the coast of Britain ? Statistical self-similarity and frational dimensions. Lengden av kysten er avhengig av lengden av målestaven, og lengden blir uendelig med en infinitisemal målestav. Seinere skrev Mandelbrot boka Fractal geometry in nature (1982). Hausdorff-dimensjonen (Felix Hausdorff) for et punkt, linje, kvadrat og kube er henholdsvis 0, 1, 2 og 3, men fraktaler kan ha ikke-heltalls dimensjoner.
Man finner fraktaler i greining av trær, blodårer, bronkier, nerveceller (L-systemer), bregner, Romanesco-kål, i skyer, og i bark. Fraktaler er en del av kaosteorien. Fraktaler oppstår ved iterasjonsprosesser. Eksempler på fraktaler er Sierpinski triangel (slumpvandring mellom 3 punkter A, B og C som danner en trekant) , Sierpinski teppe (Waclaw Sierpinski), von Koch kurve (Helge von Koch), Mandelbrot-mengden, Julia-mengden (Gaston Julia), Menger svamp (Karl Menger), Lyapunov fraktal, Peano-kurve (Giuseppe Peano) og Cantor-mengde (Georg Cantor).

Figur Barnsley bregne er en fraktal (Michael Barnsley i Fractals everywhere (1993)). Barnsley tenkte på å bruke fraktaler i datakompresjon av digitale bilder.
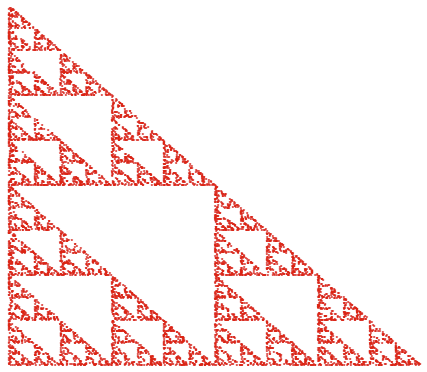
Sierpinski triangel
Det er en sammenheng mellom Mandelbrots fraktaler og kaos. Mitchell Feigenbaum (1944-2019) oppdaget i 1978 at det er en universell vei til kaos via fasetransisjoner i statistisk fysikk. Feigenbaum oppdaget at i periodedoblingen og bifurkasjonene 2, 4, 8, 16… i den logistiske avbildningen fra kvadratiske funksjoner så er forholdet mellom forskjellene i veksthastighetene r (rn+1 - rn)/(rn-2 - rn-1) ved bifurkasjoner, og dette forholdet nærmer seg Feigenbaums konstant delta(δ)= 4.66920160910299… når n går mot uendelig, et transcendeltat tall, uttrykker forhold som man finner i bifurkasjonsdiagram. Det er også en Feigenbaums kontant alfa= 2.502907876…

Bifurkasjonsdiagram for den logistiske avbildningen ved forskjellige verdier av r og bifurkasjon ved r= 3, 3.44949, 3.54409

Detalj fra kaosområdet den logististiske avbildning for verdier av r >3.5 som viser kaos avbrutt av orden.

Feigenbaums konstant vises også i Mandelbrotmengden for komplekse kvadratiske polynomer F(z)= z2 + c. Feigenbaums konstant angir forholdet mellom diameter i påfølgende sirkler i Mandelbrotmengden langs den reelle aksen i kompleksplanet.
Mandelbrot- og Julia-fraktaler er avhengig av tusenvis av iterasjoner med komplekse tall og funksjoner i et kompleksplan med en reell akse og en imaginær akse basert på det imaginære tallet i, som er lik kvadratroten av -1. Kompleksplanet må tas i bruk for å kunne forklare hva vekselstrøm er. Komplekse tall er en nødvendighet innen kvantemekanikk, og det virker som kvadratroten av -1 er en grunnleggende bestanddel innen Universet.
Hénon avbildning
Hénon-avbildning (Michel Hénon) er et tidstrinnavhengig dynamisk system som under visse betingelser er kaotisk. Avbildningen er en forenklet utgave av et Poincaré-snitt av Lorenz-avbildningen er:
\(\displaystyle x_{n+1} = 1 – a{x_n}^2 + y_n\)
\(\displaystyle y_{n+1} = bx_n\)

Figur for den klassiske utgaven er avbildningen med a = 1.4 og b = 0.3 og vi lar økning i n følge en tidsparameter t.
Hénon-avbildningen er en fraktal med Hausdorff dimensjon 1.26.
Kaos finner man også i Burgers avbildning.
Hénon M. A two-dimensional mapping with a strange attractor. Comm.Math.Phys. 50 (1976) 69-77.
Alle differensialligningene er løst i odesolveren lsoda i R-pakken "Desolve")
R Core Team (2014). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL http://www.R-project.org/.