Alderstrukturen beskrives av relativt antall individer i hver aldersgruppe. Generasjonene overlapper hverandre hvis livslengden er større enn tiden det tar for å bli voksen og reprodusere seg. Dødsraten er størst for de yngste og eldste. Fødselsraten er størst for individer i mellomalder. Aldersspesifikk fertilitetsrate er antall avkom for hver hunn på et spesifikt alderstrinn. Hvis populasjonen inneholder mange gamle ikke reproduktive individer så vil populasjonen vokse sakte. Jo kortere generasjonstid desto raskere vil populasjonen vokse.
Generasjonstiden er tiden mellom et individs fødsel og inntil det selv får avkom. Det er et forhold mellom de to kjønn i populasjonen. Antall hunner er det som vanligvis bestemmer antall fødsler. En hann kan befrukte flere hunner. For monogame arter vil antallet hanner ha større betydning.
Livshistorie er en livslang timeplan for bruk av ressurser for å få maksimal tilpasning hos arten. Inndeling i ett- og flerårige planter er et eksempel på livshistorie. Mellom vekstform og funksjon er det en genetisk fast binding. Det finnes en grunnstruktur og en grunnfunksjon i det som defineres som livsformen plante. Det er en dynamisk vekselvirkning mellom voksested, oppbygning og livssyklus til planten, kalt en livshistoriestrategi. En strategi består av forskjellige strategielementer f.eks. sukkulens og CAM-metabolisme.
Livstabeller beskriver hvordan dødeligheten varierer med alderen over tid som tilsvarer maksimal levetid. Livstabellen viser dødelighetsrate for en kohort, og beskriver i hvilke aldersstadier dødeligheten er størst. Livstabellen oppsummerer demografisk informasjon om aldersklasser. Livstabellene lages ved å følge skjebnen (mortalitetsraten) til en gruppe/kohort og nye individer inntil alle er døde. En kohort vil si at alle individene er født på samme tid, eller man kan angi antall hunner. Det går også an å bestemme alderen til et utvalgt antall individer.
Det er to hovedtyper livstabeller: Kohort livstabell hvor en gruppe individer født på samme tid følges gjennom hele livsløpet, og antall overlevende i hver aldersklasse bestemmes. I en statistisk livstabell bruker man de samme dataene, men fra hele populasjonen.
I sin livshistoriestrategi vil artene allokere ressurser i forskjellige stadier av livssyklus. Antall overlevende i hvert aldersstadium sier noe om livshistoriestrategien. Noen arter har stort antall avkom, men hvor få overlever. Andre arter har få avkom, men hvor mange av dem overlever. En raskt voksende populasjon er bunntung med et stort antall unge individer. Kjenner man vekstrate, antall individer, aldersfordeling, rekruttering, dødelighet i hver gruppe, gjennomsnittsvekt i hver gruppe er det mulig å konstruere livstabeller. Man kan studere en gruppe individer fra samme aldersgruppe (kohort) og følge denne videre ved forskjellige tidspunkter gjennom livsløpet. Livstabellen består av aldersintervall med antall levende og dødsrate for hvert aldersintervall. Man kan lage et estimat for sannsynligheten for at et individ i en årsklasse skal overleve. Overlevelse er sannsynligheten for at et individ i en populasjon eller kohort skal overleve til en bestemt alder. Dette kan fremstilles grafisk med logaritmen til antall overlevende på y-aksen versus alder på x-aksen.
Overlevelseskurver viser antall individer i kohorten som fremdeles er i live. Det finnes vanligvis tre typer overlevelseskurver.
Type I overlevelseskurve er flat for unge og middelaldrene og synker raskt når dødsraten øker hos de eldre. En type er intermediær med tilnærmet konstant død i løpet av levetiden.
En tredje type har høy dødelighet for de unge etterfulgt av en lavere dødsrate. Denne typen finnes hos arter som produserer et stort antall avkom, men ikke har yngelpleie.
Noen kan ha korte perioder med stor dødelighet f.eks. krepsdyr under skallskifte, etterfulgt av lavere dødelighet når skallet har blitt hardt. Den gjennomsnittlige levealder blir lav hvis det er stor barnedødelighet. Den potensielle levealder for mennesket er ca. 100 år, men den realiserte levealder kan være f.eks. 82 år. I fangstkurver for fisk angir man antall individer i hver årsklasse.
Det er en foreldre-avkom konflikt i den optimale investering i avkommet uten at foreldrene taper så mye i vekt og ressurser at de ikke er i stand til å reprodusere seg seinere. Foreldrene har likt slektskapsforhold til avkommet.
Demografi
Demografi er studiet av aldersstruktur (antall individer i forskjellige aldersklasser) og fertilitet til populasjoner av planter og dyr, inkludert mennesker. Antall eller relativ forekomst av individer i de forskjellige aldersklassene kan organiseres i livstabeller. Hos mange arter det det egne livshistoriestadier som egg, larve og voksen (adult). For insekter blir ikke alder like viktig, men også i hvilket stadium organismen befinner seg: egg, larve, puppe og imago. Mange krepsdyr har forskjellige larvestadier. I slike tilfeller er det mange faktorer som påvirker overgangen mellom livsstadier.
Det har stor interesse å kunne prediktere aldersstruktur og fertilitet i ressursforvaltningen av til høstbare populasjoner av krepsdyr, fisk og pattedyr. Menneskepopulasjonen har interesse for politikere i planlegging av barnehageplasser, skoler, boliger, infrastruktur og aldershjem, samt for aktuarer (forsikringsmatematikk). Populasjonen av plante- og dyreplankton, maneter i økende mengde og planktonspisende fisk kan brukes til å prediktere biomasseproduksjon.
Aldersbasert demografi kan studeres ved hjelp av Leslie-matriser. En populasjonsprojeksjonsmatrise (transisjonsmatrise) består av sannsynligheten for at et individ kommer over fra en aldersklasse til den neste. Vanligvis er matrisene basert på antall hunner, og potensielt reproduktivt hunnlig avkom. Vanligvis vil både fødsels- og dødsrate variere med alderen til individene i populasjonen.
Nedenfor er brukt betegnelsene hentet fra Gotelli, N.J.: A primer of ecology (3ed.),Sinauer Associates 2001.
Man må skille mellom alder (x) og aldersklasse (i).
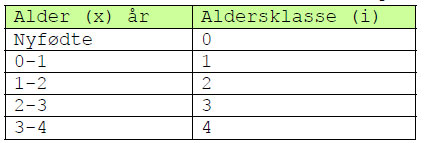
Et individ i aldersklasse i har alder mellom i-1 og i.
Vi betegner et individ med alder x som f(x), e.g. f(4) er et individ med alder 4 år. Men fi er et individ i aldersklasse i, dvs. f4 er et individ med alder mellom 3 år og 4 år. Den endelige alder til individene i populasjonen betegnes k, slik at alder x=[0,k] og aldersklasse i=[1,k].
Lotka utviklet i 1911 en kontinuerlig populasjonsmodell basert på hunnene i populasjonen. I de fleste tilfeller er det hunnenes evne til å reprodusere seg som er den begrensende faktoren.
Fekunditet, per capita fødselsrate b(x) for hunner med alder x, angir gjennomsnittet av antall hunnlige avkom (q) for en hunn i en bestemt alder, e.g. b(5)=2 vil si en hunn med alder 5 år gir gjennomsnittelig 2 hunnlig avkom. Fekundidet (l. fecunditas) betyr fruktbarhet, og sier noe om populasjonens evne til å få avkom.
Semelopare arter reproduserer seg bare en gang (monokarpe) e.g. vanligvis laks, ørkenplanter og ettårige planter. Fødselsraten blir for semelopare 0 for alle aldersklasser unntatt ved reproduktiv alder. Iteropare arter reproduserer seg flere ganger under livssyklus, som mange dyr og flerårige planter. Organismer med stort kroppsvolum trenger lenger tid på å nå reproduktiv alder, sammenlignet med små organismer.
Populasjonsveksten er avhengig av dødsraten i de forskjellige aldersklassene, det vil si overlevelse.
Overlevelse l(x) vil si sannsynligheten for at et individ overlever fra fødsel til begynnelsen av alder x. Evolusjonen påvirker både l(x) og b(x), og det er en avveining mellom reproduksjon og overlevelse. r- og K-seleksjon har sin opprinnelse fra de to konstantene i den logistiske vekstligning. Organismer som lever i et kronisk overbefolket miljø har K-seleksjon, og det er gunstig å være stor. r-selekterte arter har høy veksthastighet (r), mange avkom, for eksempel frøugras på nypløyd mark. Pionérarter trives i et ustabilt ugjestmildt miljø. Naturlig seleksjon favoriserer individer som reproduserer seg i ung alder. Er det stor investering i reproduksjon er det mindre energi tilgjengelig for vekst og ressurssikring.
Overlevelse l(x):
\(l(x)= \frac{S(x)}{S(0)}\)
Ofte studerer man en kohort av individer, alle født til samme tid, S(x) er kohortoverlevelse, og l(x) er andelen av startkohort som overlever til start av neste alder x.
Overlevelsesannsynlighet g(x) er sannsynligheten for å overleve fra alder x til alder x+1.
\(g(x)= \frac{l(x+1)}{l(x)}\)
Forskjellige arter kan ha overlevelsekurver av type I (høy overlevelse hos unge individer, lav hos eldre) , II (konstant overlevelse med økende alder) eller III (lav overlevelse for unge individer og økt overlevelse med økende alder).
Man kan beregne netto reproduktiv rate R0, gjennomsnittlig antall hunnlige avkom produsert per hunn gjennom hele livsløpet, b(x) er per capita fødselsrate, og l(x) er overlevelse:
\(R_0= \displaystyle\sum_{x=0}^k l(x)b(x)\)
Hvis R0>1 er det netto tilskudd av hunnlig avkom i generasjonen. R0=1 er en populasjon i balanse, som verken øker eller minker. R0<1 er en populasjon som går mot utryddelse (ekstinksjon). R0 tilsvarer lambda (λ) i den eksponentielle vekstmodellen, økningsraten per tidsenhet.
Generasjonstid G brukes om populasjoner med kontinuerlig vekst, gjennomsnittsalderen til foreldre til avkom laget av en kohort, måleenhet tid.
\(G=\displaystyle\frac{\sum_{k=0}^k l(x)b(x)}{\sum_{k=0}^k l(x)b(x)}\)
Generasjonstiden G>1 og for vekstrate r får man for en populasjon som vokser eksponentielt, hvor NG/N0 er ca. lik reproduktiv rate R0, får man et estimat av r:
\(N_G= N_0e^{rG}\;\;\;\; \implies\; \frac{N_G}{N_0}=e^{rG}\;\;\; \implies\: R_0\approx\; e^{rG}\;\; \implies \ln(R_0)= rG\;\implies\; r=\frac{\ln R_0}{G}\)
Euler-Lotkas demografiske ligning kan brukes til å bestemme r mer nøyaktig, den eneste ukjente i ligningen.
\(1=\displaystyle\sum_{x=0}^k e^{-rx}l(x)b(x)\)
Her er et simulert eksempel på en livstabell, hvor de tre første kolonnene er kjente data:
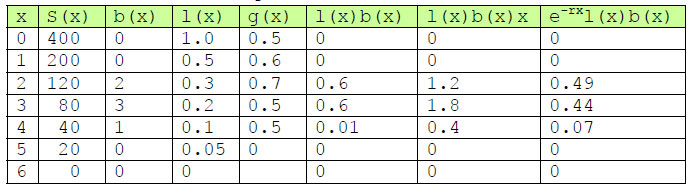
Fra r er det mulig å beregne populasjonsstørrelsen, men vi er mer interessert i å beregne antall individer i hver aldersklasse og kunne fremtidsbeskrive (prediktere) hvordan populasjonen endrer seg fra en tidsperiode n(t) til den neste n(t+1).
Vi lar ni(t) være antall individer i aldersklasse i ved tid t. Antall individer i de forskjellige aldersklassene ved tid t representert med en kolonnevektor n(t) med k aldersklasser blir:
\(N(t)=\left(\begin{matrix} n_1(t)\\ n_2(t)\\ n_3(t)\\ \vdots \\n_k(t) \end{matrix}\right)\)
Vi må kjenne til overlevelsessannsynligheten Pi for en alderklasse i. Det vil si sannsynligheten for at et individ i aldersklasse i vil overleve til aldersklasse i+1. Vi må også beregne fertiliteten Fi for hver aldersklasse. Vi må gjøre noen forenklinger for å kunne beregne Pi og Fi fra fødselrate b(x) og overlevelse l(x). Vi antar at individene telles like etter fødsel og at fødselen skjer ved overgang til en ny aldersklasse (fødselspulsmodell).
På samme måte som vi beregnet overlevelsesannsynlighet for alder x, aldersspesifikk overlevelse g(x), kan vi med forutsetningene nevnt over, beregne overlevelsessannsynlighet Pi for en alderklasse i. Vi tar ikke med aldersklasse i=0:
\(P_i= \frac{l(i)}{l(i-1)}\)
Deretter kan man beregne antall individer i en aldersklasse ni(t) til den neste ni+1(t+1) for et tidsrom t til t+1 ifølge:
\(n_ {i+1}(t+1)= P_in_i (t)\)
Fertiliteten til en alderklasse Fi blir fødselsraten i aldersklassen b(i) multiplisert med overlevelsessannsynligheten for aldersklassen.
\(F_i= P_ib(i)\)
Antall nye avkom kan beregnes som summen for alle aldersklassene:
\(n_1(t+1)=\displaystyle\sum_{i=1}^k F_in_i(t)\)
Antall individer i neste aldersklasse blir:
\(n_1(t+1)= P_1n_ 1 (t)\)
osv. for de videre aldersklassene.
Patrick H. Leslie (1945) tok i bruk Leslie-matriser for å beskrive vekst av populasjoner med aldersstruktur. Hvis det er k aldersklasser er en Leslie-matrise L en kvadratisk kxk atrise. En Leslie-matrise med 6 aldersklasser blir:
\(L= \begin{pmatrix} F_1& F_2 & F_3 & F_4&F_5& F_6 \\ P_1& 0& 0& 0& 0& 0\\ 0&P2 & 0&0&0&0\\ 0& 0& P_3& 0&0&0&\\ 0&0&0&P_4&0&0\\ 0&0&0&0&P_5&0\\ \end{pmatrix}\)
Fertilitetene for de forskjellige aldersklassene Fi står i første rad. Subdiagonalen inneholder overlevelsessannsynligheten Pi for aldersklassene. Diagonalen blir 0 siden individer kan ikke være i samme aldersklasse fra et år til det neste. Kolonner gir alder ved tid t og radene ved tid t+1.
Nå kan man lett regne ut endring av antall individer i de forskjellige aldersklassene ved matriseregning:
\(n(t+1)=L \cdot n(t)\)
Vi kan gå tilbake til eksemplet foran, men hvor vi nå ser på aldersklasser, og starter med aldersklasse 1:
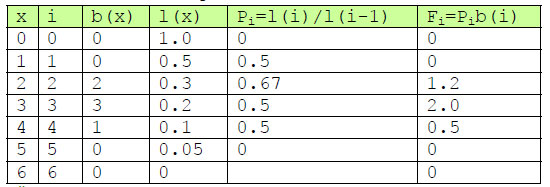
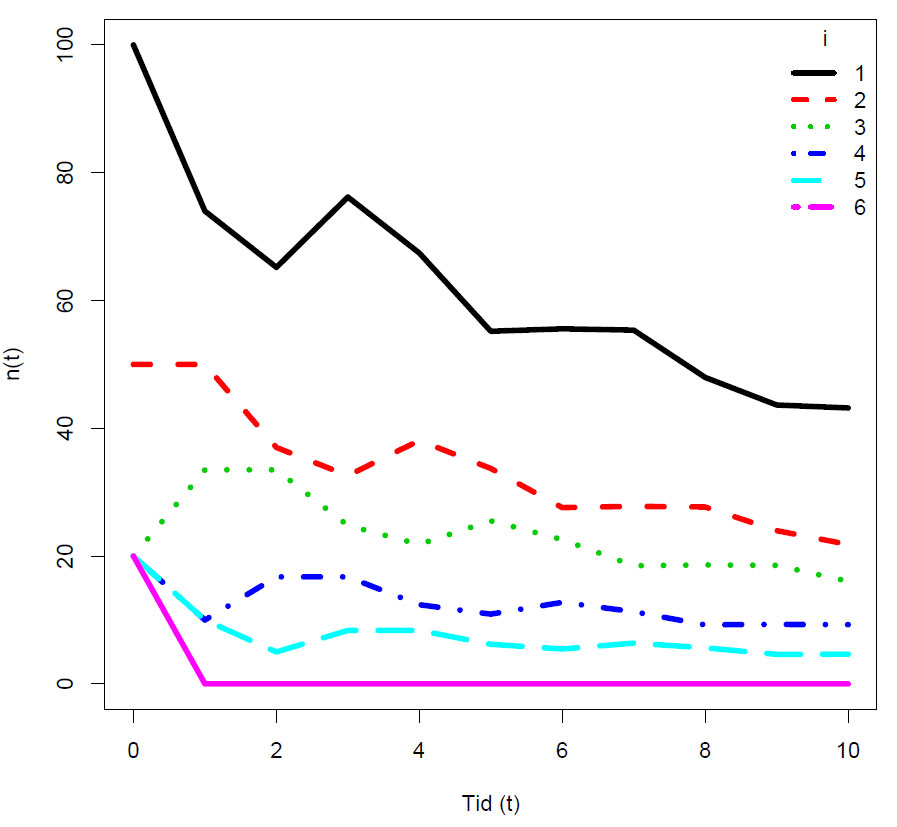
Simulert populasjonsutvikling. I dette tilfellet synker antall individer i alle aldersklassene over tid. Hvis det er konstant fødsels- og dødsrate så vil populasjonen konvergere mot en stabil aldersfordeling hvor relativt antall individer i hver aldersklasse forblir konstant, mens det absolutte antall individer øker.
Vi ser at r viser en synkende trend.
Vi finner r fra Leslie-matrisen ved først å finne totalantall individer i alle aldersklassene ntotal(t). Deretter beregnes lambda (λ):
\(\lambda= \frac{n_ {total}(t)}{n_ {total}(t-1)}\)
r bestemmes som:
\(r=\ln \lambda\)
Hvis det er en stasjonær aldersfordeling i populasjonen vil r nærme seg en konstantverdi. r kan også beregnes fra b(x) og l(x), og verdiene man får kan sammenlignes.
Parringssystemer og ressurser
Kjønnet formering gir rekombinasjon og utveksling av genmateriale som fører til variasjon. Variasjon er en forutsetning for seleksjon og adaptering til det ytre miljø. De fleste arter har kjønnet formering, men mange kan i tillegg formere seg vegetativt. For de fleste arter med kjønnet formering er kjønnsforholdet ca. 1:1, like mange hanner og hunner (Fisher-forholdet). Avvik fra dette vil gi frekvensavhengig seleksjon av det mest sjeldne kjønnet, som bringer forholdet tilbake til 1:1. Det kan være avvik fra dette forholdet hvis det skjer innavl, eller hvor miljøet bestemmer kjønnet. Noen krepsdyr og krypdyr er hermafroditter.
Hermafroditter er både hann og hunn, men også her skjer vanligvis kryssbefruktning (utkrysning), selv om selvbefruktning også er mulig. Selvbefruktning kan hindres av selvkompatibilitetsgener. Noen arter som krepsdyr og fisk har sekvensielt skifte i kjønn. Er moren i dårlig tilstand favoriseres døtre.
Monoike planter har atskilte hann og hunn på samme individ. Dioike har atskilte hann og hunn, men på atskilte individer. Forholdet mellom pollen og frøemner har betydning i utvikling av krysningssystemer hos planter.
Hos dyr er hunnens reproduktive suksess avhengig av hvor mange egg som lages. Egg krever mer ressurser. Hannens reproduktive suksess avhenger av hvor mange egg han kan befrukte. Små gameter krever mindre ressurser. Det er kompromiss mellom nåværende og fremtidig reproduksjon, og antall og størrelse på avkommet. Større individer har større sjanse til å overleve. Ressurser kan gi umiddelbar reproduksjon, eller ved forsinket reproduksjon vil ressursene først brukes til vekst som øker konkurranseevnen, og hvor ressurser brukes til opprettholdelse og økt overlevelse. Arter som reproduserer seg tidlig får kort generasjonstid. Strategien er vekst versus fruktbarhet og reproduksjon. Økt fruktbarhet reduserer vekst og derved fruktbarheten over tid. Kortlivete arter satser på fruktbarhet i stedet for vekst. Hvis de voksne har høy dødelighet kan det være en fordel å satse på stor reproduksjon tidlig. Langlivete arter investerer vekst i stedet for umiddelbar reproduksjon. Ressursbegrensninger reduserer antall avkom. Det er variasjon i hvor mange ganger reproduksjon skjer i løpet av et livsløp. Semelpare reproduserer seg en gang, iteropare flere ganger. Fordel med semelpare planter er at frøpredatorer ikke utvikles.
Aldring
Aldring er redusert fysiologisk funksjon med økende alder som gir redusert overlevelse og fertilitet med alderen. Høy dødelighet gjør at få individer blir gamle, men hvorfor varierer alderen ? Hvorfor eldes og dør organismene ? Levealder blir påvirket av naturlig seleksjon. Aldring kan skyldes akkumulering av skader i celler og vev som ikke kan repareres. Ifølge evolusjonsteori er dette et kompromiss mellom energi til reproduksjon og reparasjon. Aldersraten samstemmer med metabolsk rate. Det er mange hjerteslag hos fugl og dette kan være korrelert med kort levealder.
Litteratur:
Hughes, K.A., Alipaz, J.A., Drnevich, J.M., & Reynolds, R.M.: A test of evolutionary theories of aging. PNAS 99 (2002)14286-14291.
Walker, D.W., McColl, G. & Jenkins et al. Evolution of lifespan in C.elegans. Nature 405 (2000)296-297.
Deler av teksten er hentet fra Økologi
Menneskepopulasjonen i Norge
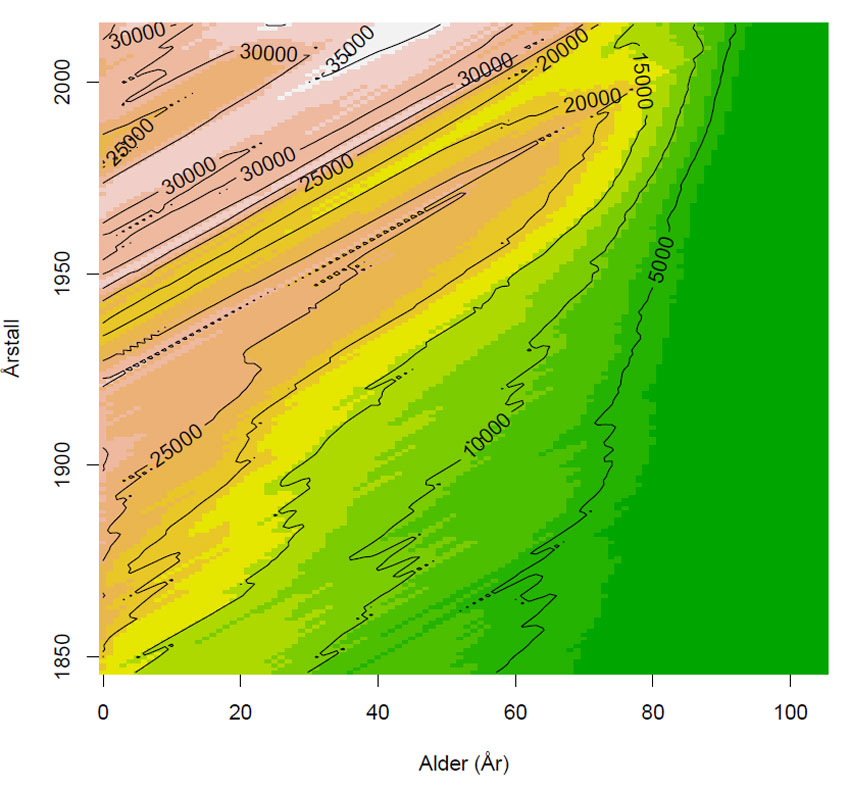
Figur 1. Konturplot som viser aldersfordelingen (0-105 år og eldre) av kvinner i Norge versus årstall (1846-2015), og antall kvinner er angitt i konturlinjene (isolinjer). Figuren viser hvordan levealderen på kvinner øker, og at fødselstallene sank under den andre verdenskrig (skrå gul linje fra ca. 1940-1945). Årsklassene > 67 år i 2015 er den framtidige pensjonistgruppen. Data SSB: Tabell 10211: Folkemengde, etter alder, kjønn, tid og statistikkvariabel .

Figur 2. Antall kvinner og menn i Norge i perioden 1846-2015. Etter år 2000 er det økende antall menn i forhold til kvinner, og for første gang i perioden er det nå flere menn enn kvinner i Norge. Data SSB: Tabell 10211: Folkemengde, etter alder, kjønn, tid og statistikkvariabel .
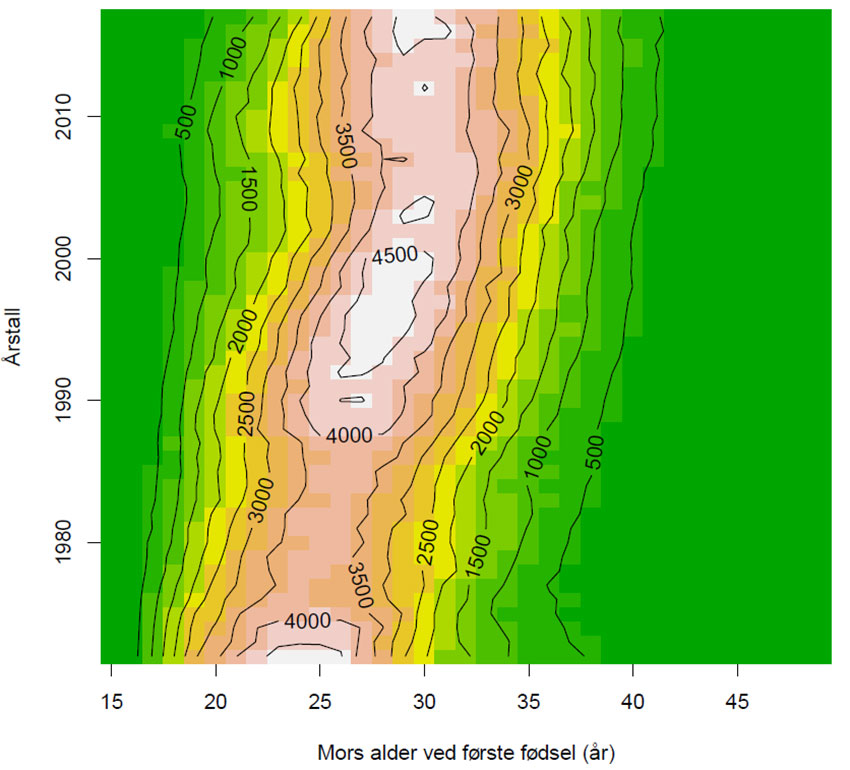
Figur 3. Mors alder (år) i Norge ved første fødsel ved forskjellige årstall. Som resultat av at dyktige kvinnene nå inntar utdanningsinstitusjonene, skaffer seg utdannelse og egen lønnsinntekt, så øker alderen for første fødsel, en trend som gjelder hele Europa, men dessverre ikke deler av Afrika og Asia. Figuren viser også hvordan fødselstallene sank omkring 1980-tallet. Data SSB: Tabell 06990 Levendefødte, etter mors alder. Politikeres krav om at nå må norske kvinner føde flere barn, er en meget kortsiktig, korttenkt løsning, og forflytter problemene bare til neste generasjon.
Antall forfedre og formødre
Slektsgranskning er en populær aktivitet, og biologisk arv betyr mye. Et barn har vanligvis to foreldre, fire besteforeldre, 8 oldeforeldre, 16 tippoldreforeldre, 32 tipp-tippoldeforeldre osv. La oss si at generasjonstiden i gjennomsnitt er 25 år og la foreldregenerasjonen være generasjon F1, besteforeldre generasjon F2 osv.
Hvor mange formødre og forfedre har du egentlig den dagen du ble født ? Foreldrene din var da i gjennomsnitt ca. 25 år og besteforeldrene ca. 50 år gamle. Du må gjerne øke generasjonstiden hvis du ønsker.
Generasjon Forfedre/formødre Tid (år)
1 2 25
2 4 50
3 8 75
4 16 100
5 32 125
6 64 150
7 128 175
8 256 200
9 512 225
10 1024 250
11 2048 275
12 4096 300
13 8192 325
14 16384 350
15 32768 375
16 65536 400
17 131072 425
18 262144 450
19 524288 475
20 1048576 500
Det vil si at for 500 år siden, 20 generasjoner, og år 1510, hadde du over 1 million forfedre og formødre. Legg på noen generasjoner til og du skjønner at snart har du flere forfedre og formødre enn det var befolkning på den tiden. Hvordan er dette mulig ? Det må ha vært et betydelig innslag av innavl, med tabubelagt incest (blodskam), kopulering av avkom mellom kusine-fetter, onkel-niese, tante-nevø, far-datter, mor-sønn, etc. Dessuten var det ikke så lett å finne ut om man giftet seg med tremenninger, firmenninger, og videre utover. Ganske mange av oss er i familie med Djengis-Khan. Den første fullstendige folketellingen i Norge var i 1769, og viste 723618 innbyggere. I 1510 var Norge i union med Danmark, styrt av kong Hans, fra slekten Oldenburg.
Darwin oppdaget at innavl hos dyr og planter gir mindre livskraftig avkom (innavlsdepresjon), mens krysning mellom homozygote foreldrelinjer gir heterose (hybridstyrke) og mer livskrafig avkom. Generelt gir hybrider mellom forskjellige arter sterilt avkom, men innen samme art kan det gi mer levedyktig avkom. Det er naturlig å tenke seg at krysning mellom menneskelinjer med større grad av homozygoter på samme måte som hos planter kunne gi hybridstyrke. Innavl gir mindre heterozygoti og mer homozygoti. Homozygoter har to like alleler for hvert gen, og dette øker sannsynligheten for at recessive egenskaper kommer til uttrykk. Mange sykdommer har recessive alleler, vi er bærere av mange av disse, de er vanligere enn man tror, men blir vanligvis undertrykt av det dominante allelet. Hvordan de to allelene, en fra far og en fra mor, blir uttrykt kan også bli påvirket av miljøet under tidlig fosterutvikling (epigenetikk), en form for Lamarchisme, som man tidligere hadde avskrevet var mulig. Ved epigenetikk skjer det ikke endringer i nukleinsyresekvensen, men både basen cytosin og histoner kan bli metylert eller demetylert, sistnevnte også acetylert/deacetylert.
Det er blitt sagt av mange av oss må være i slekt med Dsjengis-khan som levde på begynnelsen av 1200-tallet eller Bronsealdermannen funnet i Alpene, og som levde for ca. 6000 år siden. ”Setesdalrykkja” er navn på en sykdom som viser hva som kunne skje når foreldre i slekt med hverandre fikk barn sammen, noe som slett ikke var uvanlig i isolerte bygdesamfunn i gamle dager, med lite reisevirksomhet. Jfr. den amerikanske filmen Picnic med døden (Deliverance), fra 1972, vedkommende som spilte banjo.
Det har en biologisk forklaring den store interessen de unge jentene i ei isolert bygd viser for langveisfarende unge gutter som kommer til stedet, med tilsvarende sjalusi fra det lokale hannkjønn. Darwin studerte også seksuell seleksjon hos dyr, hunnkjønn som velger blant hannkjønn som viser sin fram styrke, utseende, kropp, posisjon og positur. Med dette argument kan man også forklare hvordan egenskapene kunne synge, spille et instrument, danse, framsi fortellinger, kunne lage tegninger eller byggverk, idag videreutviklet til lesing og skriving, og at også disse egenskapene kan gi konkurransefortrinn i den reproduktive dansen.
Slektskapsindeks angir sannsynligheten for at to individer deler en kopi av et angitt gen.
Databehandling
R Core Team (2015). R: A language and environment for Statistical computing. R Foundation for Statistical Computing, Vienna, Austria.URL https://www.R-project.org/.