Eksempler på selvorganisering innen biologi er opprinnelsen til liv, flokkatferd e.g. sverming (sveveatferd) hos svevemygg, fugleflokker, eller fiskestimer. Samfunnsstruktur hos sosiale insekter, dyr og mennesker. Spontan folding av proteiner og andre makromolekyler. Mønster på fiskehud eller pels (Turingmønstre: sebrastriper, flekker på leopard og sjiraff), plankton, skjell, eller nervesystem. Bronkienettverk i lungene. Purkinjefibre som leder elektrisitet i hjertet. Membranorganisering med fosfolipider. Helheten får andre egenskaper enn enkeltdelene. Kompleksitetsteori omfatter beskrivelse av komplekse adaptive systemer med spontan struktur mellom orden og kaos. Emergens er komplekse mønstre laget fra enkle struturer eller enkel atferd.
Abiotiske systemer med selvorganisering er vindblåste sanddyner, sandbunnmønster laget av bølger i vannkanten, elvedaltaer, eller vekst av krystaller e.g. snøkrystaller. Det kan være et romlig eller tidsavhengig mønster. Levende vesener er åpne energiforbrukende (dissipative strukturer) systemer langt fra likevekt.
Ilya Romanovich Prigogine (1917-2003) fikk 1977 nobelprisen i kjemi «for hans bidrag til ikke-likevekt termodynamikk, spesielt teorien om dissipative strukturer». Irreversibel termodynamikk går bare i en retning mot mer uorden. Prigogine arbeidet med komplekse systemer langt fra likevekt og irreversibilitet, og fant at energiforbrukende dissipative strukturer kan stabilisere systemet og hindre at det når likevekt.Prigogine avvlivet begrepet determinisme som ikke passer inn i ustabilitet og irreversibilitet (irreversibel termodynamikk).
Ved flokkatferd i stimer er en det sone rundt hvert individ, og enkeltindividene forsøker å unngå kollisjoner ved å organisere seg i samme bevegelsesretning som naboindividene, samtidig som det skjer tiltrekning og frastøting slik at intimsonen opprettholdes i samme størrelse. Fugler benytter synet i denne organisering. Fisk benytter syn og hydrodynamiske signaler registrert av sidelinjeorganet. Stimer med krill i havet benytter syn og hydrodynamiske signaler i stimen.
Svermintelligens er en kollektiv desentralisert selvorganiserende atferd, muligens drevet av feromoner og styrt av spesielle objekter i rommet. Andefugl, gjess og større fugler kan under trekket organisere seg i V-form. En dyreflokk som danner en ring for å beskytte seg mot en predator. I menneskesamfunnet er finans og økonomi eksempler på hvordan sosialpsykologi og flokkatferd gir selvorganisering. Andre eksempler innen kjemi og fysikk er krystallisering, vitrifikasjon og snøkrystaller.
Konveksjonsstrømmer og heksagonalt mønster i væske oppvarmet nedenfra og avkjølt ovenfra. Rayleigh-Bénards konveksjonsceller hvis vann oppvarmes sterkt nedenfra og kjøles ovenfra vil det være en kraftig konveksjon (varmestrømning) igjennom løsningen. Ved en bestemt energitilførsel klarer ikke systemet å konvektere all varmen. Det oppstår en ustabilitet som etter hvert danner en høyer organisering og med heksagonale struktur som leder vekk varmen mer effektivt, et bikakemønster i vannet (konveksjonsceller) som transporterer varmen lettere igjennom systemet. Slike konveksjonsceller kan danne mønster rundt Solens overflate hvor store energimengder sendes ut i verdensrommet.
Kjemiske oscillasjoner som Belousov-Zhabotinsky-reaksjoner (Boris Belousov og Anatoly Zhabotinsky) som gir bølger som beveger seg utover, kolliderer og annihilerer. Bølgefronter i Belousov-Zhabotinsky oscillerende kjemiske reaksjoner hvor transisjonsmetaller katalyserer oksidasjoner. Cerium (Ce3+/Ce4+) hvor sitronsyre er reduktant som skifter mellom fargeløs og gul Sitronsyre ble byttet ut med malonsyre. Oksiering av Ce3+ med brom (HBrO3). Brom-malonsyremengden øker, men Br- hemmer den autokatalyttiske reaksjonen.
Oscillasjoner er periodiske repeterte gjentakelser. En oscillator vil følge en periodisk bane. Oscillasjoner kan oppstå hvis et system er langt fra termodynamisk likevekt. Bølger og harmonisk bevegelse.
Cellulære automater (Conways game of life) som eksempel på kunstig liv og en selvreplikerende digital organisme som muterer og utvikler seg.
Kohonen nettverk (kart, Kohonenplot) (finske Teuvo Kohonen) som er et selvorganiserende kunstig nevralt nettverk. Blir brukt til å visualisere flerdimensjonale data.
Turing-striper, morfogen (diffusjon, aktivator, inhibitor) og Turing-mønster. Etter Alan Turing (1912-1954) kjent som matematiker og kryptograf ved Bletchley Park, løsing av Enigmakoden under andre verdenskrig, samt hypotetisk Turing-maskin. Alan Turing hadde en tragisk skjebne beskrevet i filmen The imitation Game (2014). Turing-mønster i værsystemer, galakser, og fargemønster på overflaten av fisk (flekker, striper, spiraler).
På samme måte har økosystemene strukturer som gir mest mulig effektiv energigjennomstrømning.
Systemet omorganiseres når gjennomstrømningen av energi blir for stor. I utgangspunktet er sannsynligheten for å skape orden fra uorden uendelig liten, men ved stor gjennomstrømning av energi gjennom systemet kan det skje.
Forutsetningene for selvorganisering er:
1. Åpent system som har flukser med stoff og energi
2. Systemet er fjernt fra likevekt
3. Ikke-lineære sammenhenger mellom flukser og krefter.
Dette må kobles til arv av økt orden, gjensidig avhengighet og Darwinistisk seleksjon.
Det er en nær sammenheng mellom selvorganisering og irreversibel termodynamikk, også med tilknytning til kunstig intelligens (AI), kunstige immunsystemer og neurale nettverk som kan lære og huske. Med genetiske metaheuristiske (gr. hauriskein – finne fram) algoritmer (regneregler) og interasjonsprosesser som etterligner naturlig seleksjon, evolusjonsalgoritmer, er det mulig å studere dynamikken i evolusjonen.
Alle biologiske, kjemiske og fysiske systemer endrer seg over tid, de er dynamiske og kan bli beskrevet av tilstandsvariabler i en eller flere differensligninger med og diskrete tidstrinn, eller som differensialligninger med kontinuerlig tidsutvikling. Systemene blir drevet dissipative strukturer (energiforbrukende systemer), gradienter i energi og potensial, for eksempel kjemisk potensial i form av trykk (kinetisk energi), konsentrasjon, høyde (potensiell energi, kjemisk stillingsenergi) eller elektrisk ladning. Gibbs fri energi, ΔG, er et mål på mengden energi som er tilgjengelig for å utføre arbeid, angitt med måleenheten joule (J) per mol.
Biologiske systemer og irreversibel termodynamikk
De levende biologiske systemene er åpne, ustabile og langt fra termodynamisk likevektstilstand, på lignende måte som værsystemer. Ustabile systemer kan bare beskrives og uttrykkes som statistiske sannsynligheter. Systemene blir gjennomstrømmet med flukser av stoff og energi, beskrevet av irreversibel termodynamikk. En fluks angir mengden stoff eller energi som passerer per areal- og tids-enhet. Kjernereaksjoner i Sola hvor massetapet når hydrogen blir omdannet til helium gir bl.a. elektromagnetisk stråling med bølgelengder fra ca. 260 til 850 nanometer (nm) i det biologiske vindu som påvirker organismene på Jorden. Klorofyll i plantene, bakterieklorofyll hos bakteriene, fykobiliproteiner i blågrønnbakterier og rødalger, samt karotenoidene absorberer deler av den elektromagnetiske strålingen fra Sola, og fanger den i form av elektroner og protoner fra vann, som reduksjonskraft (NAD(P)H og kjemisk energi (ATP). Oksygen blir et biprodukt i reaksjonen, og virker som en elektron- og proton-akseptor når energien som ligger i de organiske molekylene blir frigitt i den respirative oksidasjonsprosessen og vann blir dannet på nytt. Reduksjonskraften og den kjemiske energien fra lysreaksjonen i fotosyntesen blir brukt til å redusere CO2 til organiske forbindelser, som inneholder et lager av elektroner og protoner med opprinnelse fra vann.
Heterotrofe organismer som sopp, dyr og mennesker bruker fotosynteseproduktene som energikilde, men i hvert trinn tapes det energi. Hos dyr og mennesker blir energien i fotosynteseproduktene overført til varme (termisk energi), bevegelsesenergi (arbeid, mekanisk energi) og til å drifte hjerne- og tankevirksomhet (elektrisk energi). Varmeenergien forflytter seg bare i en temperaturgradient fra varmt til kaldt (termodynamikkens andre lov sier at motsatt vei er umulig). Varmen (termisk energi) går ut i atmosfæren og videre ut i verdensrommet. Termodynamikkens første lov sier at total mengde energi i universet er konstant, mens termodynamikken andre lov (Carnot-prinsippet) sier at kvaliteten på energien minker. Det er et hierarki av energiformer hvor man på toppen har fysisk-, kjemisk- og elektrisk energi, og på bunnen varmeenergi, den med lavest kvalitet og blir derved vanskelig å utnytte. De biologiske systemene kan selvorganisere seg ved å eksportere entropi til omgivelsene (de dissiperer). Begrepet entropi danner basis for irreversibilitet. Schrödinger kalte den informasjonen som ligger i den orden som finnes i organiske molekyler for negentropi. Metabolismen bruker en ytre kilde (mat hos dyr, lys hos planter) med negentropi (jfr. Erwin Schrödinger What is life ?) for å kunne opprettholde eget liv og vekst. En membran skiller og beskytter de levende system fra omgivelsene. Det er et replikerende system med RNA eller DNA som lagrer informasjon om organismen og overfører kopier med variasjon til et avkom. Manfred Eigen mente med Eigen-Schuster hypersykler å kunne forklare utvikling av liv, selvorganisering og evolusjon med autokatalytiske sykler, kalt hypersykler.
Ilya Romanovich Prigogine (1917-2003) fikk nobelprisen I kjemi i 1977 for sitt arbeid med irreversibel termodynamikk og dissipative systemer (energiforbrukende systemer). Prigogine avliver begrepet determinisme som ikke passer inn i ustabilitet og irreversibilitet. Han ser også likhetstrekk med variasjon hos individene til utvikling av populasjonen, på lignende måte som Ludwig Boltzmann betrakter gasser som en populasjon med partikler (makrotilstand), ikke som enkeltpartikler(mikrotilstand).
Attraktor
Ikke-lineære ligninger er vanskelig å løse analytisk. De numeriske løsningene av ligningene kan bli visualisert geometrisk i to eller tre dimensjoner i et faserom i form av integrallinjer (løsningslinjer, trajektorier). Den franske matematikeren Henri Poincaré (1854-1912) var en av dem som viste fordelen med visualiserte geometriske løsninger av ligningene. Trelegemeproblemet er vanskelig å løse matematisk og man tyr derfor til approksimasjoner (tilnærminger). Trajektoriene eller løsningslinjene er glatte linjer, og de kan aldri krysse hverandre i planet, for i ethvert punkt på kurven finnes det bare en tangent eller derivert. I et tidsseriediagram kan man vise trajektoriene med en tidspil fra fortid, via nåtid, til prediktert og modellert framtid. En attraktor er en samling med numeriske verdier i faserommet som systemet beveger seg mot. En attraktor kan være ett eller flere punkter, en kurvatur, overflate, manifold eller en fraktal. Sistnevnte kalles en underlig attraktor (”strange attractor”) som observeres i dynamiske systemer som opptrer kaotisk med kaotiske trajektorier (løsningslinjer), men som i visse områder opptrer periodisk og forutsigbart. For den logistiske funksjonen er attraktoren et eller to punkter representert som bæreevnen til systemet.
En attraktor representerer en stabil likevekt, hvor alle trajektoriene blir samlet. To attraktorer gir fluktuasjoner som bifurkasjoner. Akkurat som alt konvergerer mot maksimal entropi, som en pendel som svinger fritt vil etter noen oscillasjoner henge rett ned uansett startbetingelser. Hvis trajektoriene flyter motsatt vei, vekk fra en attraktor, så kalles de en repellor. Med en kaotisk attraktor kan systemet være lokalt ustabilt, men globalt i større skala stabilt. I et todimensjonalt faserom er en lukket syklus eller en grensesyklus (”limit cycle”) et lukket trajektorium i en periodisk bane. van der Pol oscillatoren er et stabilt lukket system. Poincaré-Bendixon-teoremet kan brukes til å prediktere om det er et lukket syklus eller ikke.
Celler kan virke som en attraktor. Kontinuerlig attraktor nettverkteori.
van der Pol oscillator
Differensialligningene for van der Pol oscillatoren er
\(\frac{\mathrm d x}{\mathrm d t} = y\)
\(\frac{\mathrm d y}{\mathrm d t} = b\left(1-x^2 \right)y-x\)
van der Pol ligningen har en begrenset syklus for hver verdi av b > 0. Den har vært brukt i modellering av hjerteslag, solflekksyklus og pulserende stjerner (Cepheidene). Man finner van der Pol oscillasjon i en elektrisk krets utsatt for periodisk endring i spenningen.
van der Pol ligningene kan også uttrykkes som:
\(\frac{\mathrm d^2 x }{\mathrm d t^2} + b\left(x^2-1 \right) \frac{\mathrm d x}{\mathrm d t} + x=0\)
Figur. van der Pol ligningen er en begrenset syklus som avhenger av verdien for b: b=2 (rød), b=0.1 (blå), initialverdier (1,1). Sirkulært fasetrajektorium for b<1. Ved større b er trajektoriene to ganger utenfor sirkelen per syklus.
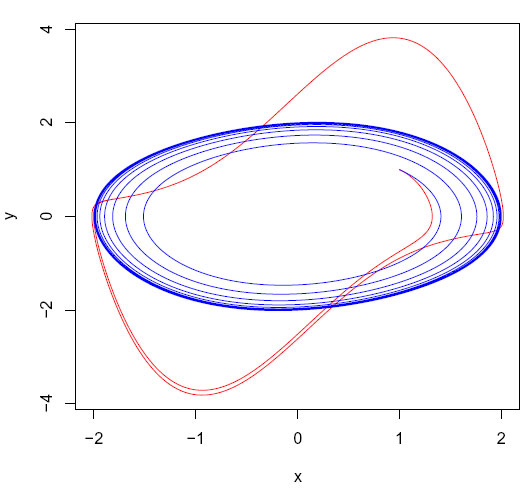
Figur van der Pol fasediagramdiagram b = 1, initialbetingelser (1,1), x(rød), y (blå)

Figur van der Pol tidsseriediagram b = 1, initialbetingelser (1,1), x(grønn), y (tomatrød). Tid t
Van der Pol, B. On relaxation oscillations. Philosophical Magazine 2 (1926) 978-992
Rössler attraktor
Rössler ligningene er et enklere system enn Lorenz uten kvadratledd, med kaotisk løsning for a=0.2, b=0.2 og c=5.7. Denne er et av de enkleste kaotiske systemene.
\(\frac{\mathrm d x}{\mathrm d t} = - y –z\)
\(\frac{\mathrm d y}{\mathrm d t} = x + ay\)
\(\frac{\mathrm d z}{\mathrm d t} = b + z \left( x-c \right)\)
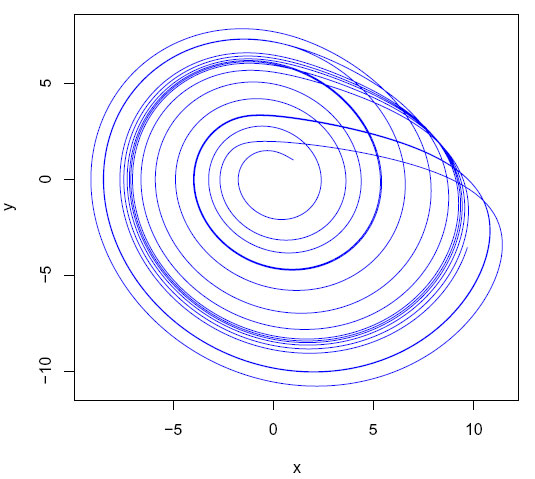
Figur. Fasediagram for Rössler ligningene og initialverdier (1,1,1). a=0.2, b=0.2 og c=5.7
Når trajektorier atskilles eksponensielt og divergerer uendelig hvordan er det mulig at de er begrenset ? Svaret er strekning og folding. Som en firkantet deig som kjevles ut til en flat deig, foldes og kjevles ut på nytt, slik at den til slutt består av en rekke tynne lag. Jfr. et wienerbrød
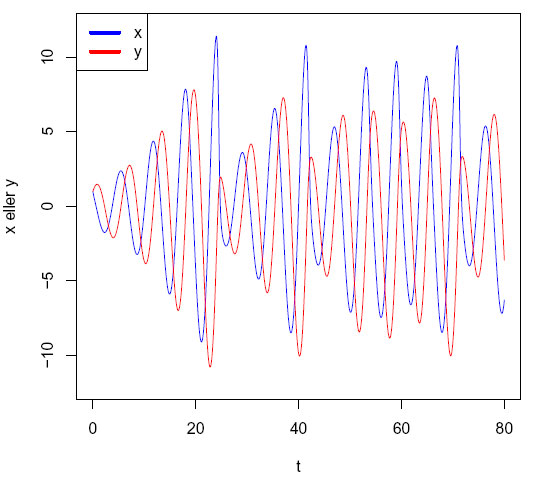
Figur. Tidsdiagram for Rössler ligningene og initialverdier (1,1,1). a=0.2, b=0.2 og c=5.7, tid t.
Rössler, O.E.: An equation for continous chaos. Phys.Lett A57 (1976)397.
Wikipedia